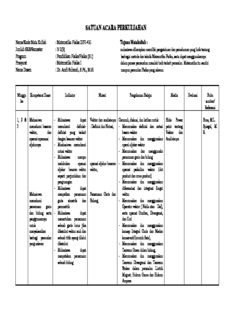
SATUAN ACARA PERKULIAHAN Nama/Kode Mata Kuliah : Matematika Fisika II/FI-431 Tujuan Matakuliah : Jumlah SKS/Semester : 3/ 2(3) mahasiswa diharapkan memiliki pengetahuan dan pemahaman yang baik tentang Program : Pendidikan Fisika/Fisika (S1) berbagai metode dan teknik Matematika Fisika, serta dapat menggunakannya Prasyarat : Matematika Fisika I dalam proses pemecahan masalah baik terkait persoalan Matematika itu sendiri Nama Dosen : Dr. Andi Suhandi, S.Pd., M.Si maupun persoalan Fisika yang relevan. Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi 1, 2 & Mahasiswa - Mahasiswa dapat Vektor dan analisisnya Ceramah, diskusi, dan latihan untuk: Slide Power Boas, M.L. 3 memahami besaran memahami definisi- : Definisi dan Notasi, - Merumuskan definisi dan notasi point tentang Spiegel, M. vektor, dan definisi yang terkait besarn vektor Vektor dan R. operasi-operasasi dengan besaran vektor - Merumuskan dan menggunakan Analisisnya aljabarnya - Maahasiswa memahami opersi aljabar vektor notasi vektor - Merumuskan dan menggunakn - Mahasiswa mampu persamaan garis dan bidang melakukan operasi operasi aljabar besaran - Merumuskan dan menggunakan aljabar besaran vektor vektor, operasi perkalian vektor (dot seperti penjumlahan dan product dan cross product) pengurangan - Merumuskan dan menggunakan - Mahasiswa dapat diferensiasi dan integrasi fungsi Mahasiswa menyatkan persamaan Persamaan Garis dan vektor memahami garis simetrik dan Bidang, - Merumuskan dan menggunakan persamaan garis parametrik Operator vektor ( Nabla atau Del), dan bidang serta - Mahasiswa dapat serta operasi Gradien, Divergensi, penggunaannya menentukan persamaan dan Curl untuk sebuah garis lurus jika - Merumuskan dan menggunakan menyelesaikan diketahui vektor arah dan konsep Integral Garis dan Medan berbagi persoalan sebuah titik ayang dilalui konservatif (contoh fisis), yang relevan diketahui - Merumuskan dan menggunakan - Mahasiswa dapat Teorema Green dalam bidang, menyatakan persamaan - Merumuskan dan menggunakan sebuah bidang Teorema Divergensi dan Teorema Stokes dalam persoalan Listrik Magnet; Hukum Gauss dan Hukum Ampere. Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi - mahasiswa dapat menentukan persamaan suatu bidang jika diketahui vektor normal bidang dan titik pada bidang - Mahasiswa dapat menentukan jarak tegak lurus dari suatu titik ke sebuah garis atau suatu bidang - Mahasiswa dapat menentukan jarak antar bidang. Mahasiswa - Mahasiswa dapat Perkalian Vektor; dot memaahami menyatakan kaidah product dan cross operasi perkalian perkalian titik (dot product, vektor dan hukum- product) adan perkalian Aplikasi perkalian tiga hukum aljabar silang (cross product) vektor dalam persoalan yang berlaku, dan dari dua buah besarn Fisika, penggunaannya vektor atau lebih untuk - Mahasiswa dapat menyelesaikan menyatakan hukum- berbagai persoalan hukum aljabar yang yang relevan berlaku terkait perkalian dua buah vektor atau lebih - Mahasiswa mampu melakukan operasi perkalian dua buah besaran vektor atau lebih baik operasi dot product , cross product, maupun campurannya Mahasiswa - Maahasiswa mampu memahami menyelesaikan persoalan Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi kalkulus dari Fisika terkait dengan Diferensial dan Integral besaran vektor, operasi perkalian vektor, Fungsi Vektor serta serta seperti menghitung torsi, aplikasainya, penggunaannya komponen torsi, untuk momentum sudut, dan menyelesaikan lain-lain berbagai persoalan - Mahasiswa dapat yang relevan melakukan diferensiasi dan integrasi biasa dari fungsi vektor - Mahasiswa dapat menyelesaikan persoaln fisika terkait dengan aplikasi diferensiasi dan integrasi fungsi vektor, seperti penentuan vektor kecepatan dari vektor posisi, penentuan vektor kecepatan dari vektor percepatan, dan sebaginya Mahasiswa - Mahasiswa dapat Operator vektor : Nabla memahami menyatakan operator del atau Del, Gradien, operator nabla dan (nabla) dalam berbagi Divergensi, Curl, operasinya sistem koordinat (gradien, - Mahasiswa mampu divergensi, dan mengoperasikan operator curl), serta del terhadap suatu penggunaannya besaran skalar dengan untuk opersi perkalian biasa menyelesaikan (Gradient) persoalan yang - Mahasiswa mampu relevan mengoperasikan operator del terhadap suatu besaran vektor dengan opersi perkalian titik (Divergensi) Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi - Mahasiswa mampu mengoperasikan operator del terhadap suatu besaran vektor dengan opersi perkalian silang (Curl) Mahasiswa - Mahasiswa mampu Integral Garis, Medan memahami konsep melakukan perhitungan konservatif (contoh integral garis serta integral garis dari suatu fisis), penggunaannya fungsi vektor, misalnya untuk vektor gaya. menyelesaikan - Mahasiswa dapat persoalan fisis menyatakan syarat suatu yang relevan medan vektor tergolong medan konservatif - Mahasiswa dapat Mahasiswa menguji kekonservatifan memahami medan suatu medan vektor konservatif dan - Mahsiswa adapat cara pengujian menyebutkan medan- kekonservatifan medan dalam fisis yang suatu medan vektor tergolong ke dalam medan konservatif - Mahsiswa dapat menyelesaikan persoalan fisika terkait dengan aplikasi integral garis, seperti persoalan usaha, potensial dan lain-lain. Mahasiswa - Mahasiswa dapat Teorema Green dalam memahami teorema menyatakan Teorema bidang, Green dan Green. penggunaannya - Mahasiswa dapat untuk menggunakan Teorema menyeleasaiakan Green untuk persoalan yang menyelesaikan berbagai relevan persoalan terkait baik Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi Mahasiswa Persoalan matematika Teorema Divergensi memahami teorema maupun persoalan fisika dan Teorema Stokes, Divergensi dan - Mahasiswa dapat aplikasinya dalam Stokes, serta menyatakan Teorema persoalan Listrik penggunaannya Divergensi. Magnet; Hukum Gauss untuk - Mahasiswa dapat dan Hukum Ampere) menyeleasaiakan menggunakan Teorema persoalan yang Divergensi untuk relevan menyelesaikan berbagai persoalan terkait baik Persoalan matematika maupun persoalan fisika seperti persoalan Hk Gauss dalam persoalan kelistrikan. - Mahasiswa dapat menyatakan Teorema Stokes. - Mahasiswa dapat menggunakan Teorema Stokes untuk menyelesaikan berbagai persoalan terkait baik Persoalan matematika maupun persoalan fisika seperti persoalan Hk Ampere dalam persoalan kelistrikan. Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi 4 & 5 Mahasiswa - mahasiswa dapat Kalkulus variasi : Ceramah, diskusi, dan latihan untuk: Slide Power Boas, M. L. memahami menyatakan persoalan Persoalan nilai - Memaparkan persoalan nilai point tentang persoalan nilai nilai stasioner suatu Stasioner; contoh stasioner suatu kuantitas dan syarat- Kalkulus stasioner dari suatu kuantitas fisis beserta Prinsip Fermat, syarat pengujiannya Variasi kuantitas dan syarat-syarat yang - Merumuskan dan menggunakan syarat-syarat yang diperlukannya Persamaan Euler dalam persamaan Euler dalam berbagai diperlukannya - Mahasiswa dapat berbagai jenis variabel, jenis variabel menyatakan persamaan - Merumuskan dan menggunakan Euluer dalam berbagai Integral pertama dari persamaan jenis variabel Euler Mahasiswa - Mahsiswa dapat - Merumuskan dan menggunakan memahami menuliskan persamaan Persaman Lagrange dan Prinsip persamaan Euler, Euler untuk suatu Hamiltonian utnuk menyelesaikan kegunaannya, serta persoalan nilai stasioner persoalan Mekanika penggunaannya yang dinyatkan dalam untuk bentuk integral menyelesaikan - Mahasiswa dapat persoalan nilai menggunakan persamaan stasioner suatu Euler dan alat bantu yang kuantitas diperlukannya untuk menyelesaikan berbagai persoalan terkait persoalan nilai stasioner suatu kuantitas Integral pertama dari matematis atau fisis. persamaan Euler, - Mahasiswa dapat melakukan penukaran variabel untuk membentuk integral Persaman Lagrange; pertama persamaan Euler Prinsip Hamiltonian, Mahasiswa - Mahasiswa dapat Aplikasi dalam memahami menyatakan persamaan persoalan Mekanika) persamaan Euler-Lagrange untuk Lagrange dan persoalan yang terkait prinsip beberapa variabel terikat. hamiltonian, serta - Mahasiswa dapat penggunaannya menyatakan prinsip Hamiltonian Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi Untuk - Mahasiswa dapat menyelesaikan menyelesaikan persoalan fisis persoalan-persoalan yang relevan yaitu fisika yang terkait persoalan gerak dengan penerapan benda. prinsip Hamiltonian dan persamaan Lagrange, miasalnya pada persoalan tenatang gerak partikel. TU 1 Slide Power Boas, M. L. 6 & 7 Mahasiswa - Mahasiswa dapat Deret tak hingga : Ceramah, diskusi, dan latihan untuk: point tentang Wospakrik, memahami deret menyatkan definisi- Definisi dan Notasi, - Merumuskan definisi dan notasi Deret Tak H.J tak hingga dan definisi yang terkait deret tak hingga Hingga melakukan uji dengan deret tak hingga - Merumuskan dan menggunakan kekonvergenannya - Mahasiswa dapat konsep kekonvergenan deret dan menyatakan notasi deret teknik-teknik uji konvergensi tak hingga - Memaparkan car-cara mencari - Mahasiswa dapat Persoalan pernyataan deret pangkat dari suatu menyatakan definisi kekonvergenan deret fungsi; deret Taylor dan McLaurin kekonvergenan suatu dan teknik-teknik uji serta penentuan selang deret tak hingga konvergensinya, konvergensinya - Mahasiswa dapt - Mengaplikasikan konsep deret menyatakan berbagai pangkat untuk menyelesaikan macam teknik untuk uji persoalan-persoalan Matematika dan kekonvergenan berabagai Fisika relevan deret tak hingga - Mahasiswa dapat melakukan uji konvergensi suatu deret dengan teknik pengujian yang tepat Mahasiswa - Mahasiswa dapat Pernyataan deret memahami deret menyatakan deret pangkat dari suatu pangkat tak hingga, pangkat tak hingga fungsi; deret Taylor dan cara-cara mencari McLaurin, Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi bentuk pernyataan - Mahasiswa dapat serta penentuan selang deret pangkat dari mencari selang konvergensinya suatu fungsi, konvergensi untuk deret mencari selang pangkat tak hingga konvergensinya, - Mahasiswa dapat serta menyatakan teorema- penggunaannya teoreama yang berlaku untuk untuk deret pangkat tak menyelesaikan hingga dan berbagai persoalan menggunakannya untuk yang relevan berbagai keperluan anlisis persoalan yang relevan - Mahasiswa dapat menyatakan suatu fungsi dalam deret pangkat tak hingga (deret taylor atau McLaurin) sekaligus menentukan selang konvergensinya - Mahasiswa dapat menggunakan berbagai teknik untuk mencari pernyataan deret pangkat tak hingga dari fungsi- fungsi yang kompleks - Mahasiswa dapat menyelesaikan berbagai persoalan baik persoalan Aplikasi deret dalam matematika maupun persoalan persoalan fisika yang terkait Matematika adan dengan aplikasi konsep Fisika) deret tak hingga. Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi 8 & 9 Mahasiswa - Mahasiswa dapat Deret Fourrier : Ceramah, diskusi, dan latihan untuk: Slide Power Boas, M. L. memahami deret menyatakan fungsi Fungsi Periodik, - Merumuskan definisi dan notasi point tentang Wospakrik, Fourrier dan periodik beserta ciri-ciri deret Fourrier Deret Fourrier H.J syarat-syarat agar pokoknya Nilai rata-rata Fungsi, - Merumuskan cara mencari suatu fungsi - Mahasiswa dapat dapat koefisien-koefisien Fourrier untuk periodik dapat menentukan periode Koefisien Fourier untuk pernyataan fungsi periodik dalam dinyatakan dalam suatu fungsi periodik pernyataan deret deret Fourier sinus-cosinus deret Fourrier. - Mahasiswa dapat Fourier sinus-cosinus - Merumuskan dan menggunakn menentukan nilai rata- kondisi Dirichlet rata suatu fungsi dalam - Merumuskan cara mencari selang dasarnya koefisien-koefisien Fourrier untuk - Mahasiswa dapat pernyataan fungsi periodik dalam menyatakan persamaan deret Fourier kompleks untuk mencari koefisien - Merumuskan fungsi ganjil, genap, Fourrier dari suatu fungsi dan tidak ganjil-tidak genap serta periodik cara menyatakannya dalam deret - Mahasiswa dapat Fourier Sinus, Cosinus, Sinus- mencari pernyataan deret Cosinus. Fourrier dari suatu fungsi - Merumuskan cara melukiskan periodik dalam bentuk spektrum Fourrier deret sinus-cosinus - Merumuskan dan menggunakan - Mahasiswa dapat Teorema Parseval untuk mencari menyatakan kondisi jumlah deret pangkat tak hingga Dirichlet (kondisi yang Kondisi Dirichlet, - Mengaplikasikan konsep deret harus dipenuhi agar suatu Fourrier untuk menyelesaikan fungsi periodik dapat persoalan-persoalan Matematika dan dinyatakan dalam deret Fisika yang relevan Fourrier) dan menggunaknnya untuk identifikasi fungsi. - Mahasiswa dapat Koefisien Fourier untuk menyatakan fungsi pernyataan Deret periodik dalam deret Fourrie Kompleks, Fourrier fungsi kompleks - Mahasiswa dapat menyatakan ciri-ciri Fungsi ganjil, genap, fungsi periodik genap, dan tidak ganjil-tidak Minggu Kompetensi Dasar Indikator Materi Pengalaman Belajar Media Evaluasi Buku ke sumber/ Referensi Mahasiswa ganjil, dan tidak genap- genap, memahami fungsi tidak ganjil Deret Fourier Sinus, ganjil, genap, dan - Mahasiswa dapat Cosinus, Sinus- tidak ganjil-tidak menyatakan fungsi genap Cosinus. genap serta cara dalam deret Fourrier mencari pernyataan Cosinus deret Fourrier yang - Mahasiswa dapat relevan menyatakan fungsi ganjil dalam deret Fourrier Sinus - Mahasiswa dapat menyatakan fungsi tidak ganjil-tidak genap dalam deret Fourrier Sinus- cosinus - Mahasiswa dapat mengembangkan fungsi yang didefinikan dalam setengah selang dasar menjadi fungsi geanap, fungsi aganjil dan fungsi tidak ganjil-tidak genap, Mahasiswa dan menyatakannya memahami cara dalam deret Fourrier menggambarakan terkait. spektrum Fourrier - Mahasiswa dapat untuk suatu menggambarkan Spektrum Fourier peranyataan deret spektrum Fourrier dari Fourrier dari suatu pernyataan deret Fourrier fungsi suatu fungsi - Mahasiswa dapat Mahasiswa menyatakan teorema Teorema Parseval memahami teorema Parseval Parseval dan - Maahasiswa dapat penggunaannya menggunakan teorema untuk mencari Parseval untuk