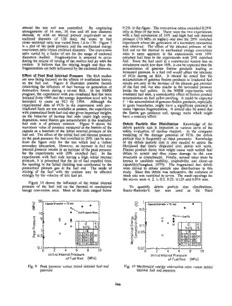
around the test rod was controlled. By employing (!.2% inthe figure. The conversion ratios exceeded I).25% arrangements of 16 mm, 30 mm and 60 mm diameter only inthree of the tests. These were the two experiments shrouds, or with no shroud present (equivalent to an with a fuel enrichment of 10% and high fuel rod internal enclosed diameter of 120 mm), the water to fuel pressure (7.0 MPa or higher) and also the 20% enriched cross-sectional ratio was varied from 1.6 to 170. Figure 7 experiment where the generation of a secondary interaction is a plot of the peak pressure and the mechanical energy was observed. The effect of the internal pressure of the conversion ratio versus enclosed diameter. The conversion fuel rod on the thermal to mechanical energy conversion ratio varied by a factor of ten for the range of enclosed ratio is more apparent in the experinaents with 10% diameters studied. Fra.gmentation is assumed to occur enriched fuel than in the experiments with 20% enriched during the course of mixing of the molten fuel jet with the fuel. Since the fuel used in a commercial reactor has an coolant. It follows that the mixing length and thus the enrichment much less than 10%, itcan be expected that the fragmentation are both influenced bythe enclosed diameter, accumulation of gaseous fission products leading to increased pressure in a fuel rod would affect the intensity Effect of Fuel Rod Internal Pressure The RIA studies of FCIs during an RIA. It should be noted that the arenow being focused on the effects of irradiationhistory accumulation of gaseous fission products in irradiatedfuel on the fuel rod. Figure 8 illustrates possible factors results not only in the increase of the plenum gas pressure concerning the influence of fuel burnup on generation of of the fuel rod, but also results in the increased pressure destructive forces during a severe RIA. In the NSRR inside the fuel pellets. In the NSRR experiments with program,the experiment with pre-irradiated fuel has been irradiatedfuel rods,aconsiderable effect of fission product initiatedfrom 1989 andthe energy deposition level will be accumulation on fuel pellet swelling. Itcould be expected increased to cause an FCI by 1994. Although the t_' ."theaccumulation ofgaseous fission products, especially experimental data of FCIs in the experiment with pre- in grain boundaries, might have a significant potential to irradiatedfuels are notavailable at present, the experiment cause vigorous fragmentation. Itshould also be noted that with pressurized fresh fuel rodalsogives importantinsights the fission gas produces soft, spongy melts which might on the behavior of burnup fuel rods under high energy have acontrary effect. deposition, since fission gas accumulation inthe irradiated fuel rods is of primary concern. Figure 9 shows the Debris Particle Size Distribution Knowledge of the maximum value of pressure measured at the bottom of the debris particle size is important in various areas of the capsule as a function of the initial internal pressure of the safety evaluation of nuclear reactors. In the computer fuel rod. The effect of the initial fuel rod internal pre_ure modeling of the damage potential of FCIs, the debris on the peak pressure for fuel enriched to 20% can be seen particle size is frequently an input parameter. Knowledge from the figure only for the test which had a violent of the debris particle size is also needed to assess the secondary interaction, ttowever, an increase in fuel rod likelihood that finely dispersed core debris will settle. internal pressure results inan increase of the peak pressure Fission product decay heat might cause such settled fuel for the experiments with 10% enriched fuel. In the debris to remelt and thus cause damage to the core experiments with fuel rods having a high initial internal structures or containment. Finally, aerosol sizes must be pressure, it is presumed that the jet of fuel expelled from known to establish mobility, respirability and clean-up the ope.nin_,in the failed cladding was accelerated by the capability(Vaughan, 1979). The fragmented fuel debris pressunzeo plenum gas in the fuel rod. The mode of were sieved to obtain particle size distributions in this mixing of the fuel with the coolant may be affected study. Since this debris was radioactive, the variation of strongly by the velocity of this fuel jet. mesh size was restricted to seven. The mesh openings for the sieves were 4, 2, 1,0.5, 0.25, (I.125 and 0.074 mm. Figure 10 shows the influence of the initial internal pressure of the fuel rod on the thermal to mechanical To quantify debris particle size distributions, energy conversion ratio. Most of the data ranged below Rosin-Rammler's law was used as the fitted CopsuleDion_ter=72mm • I I_"'_ 2ridPre_tsuerWove >,'P:, / _ v-----F-c-,2.. r o o0,L, .-_0051- Ioi i.18 _I: o ,all27t013320 n 0.:::)_ ai1'50to1152_ ..c,:_o8 ' ll" o I!h1li1i2.75t0ot1o.l3.53,2210 !" v11163tol.65 _ I- i_11163t0i.65 r ell.lifo1,22 10 ..z I le11.1!.to1.2210 01_ 001 " '0 2 4 6 8 10 ' 0 2 4 6 8 0 InitiolInternolPressure InitiolInternolPressure of FuelRod (MPo) of FuelRod (MPo) Fig. 9 Peak pressure versus initial internal fuel rod Fig. l0 Mechanical energy conversion ratio versus initial pressure internal fuel rod pressure 2_6 function(Tsuruta etal., 1985). InRosin-Rammler's law, the observation of debris by a scanning electron microscope. distribution function is given by: Another possible index for the degree of fuel fragmentation is the volume-surface mean diameter D,, defined as the R(Dt,) = 1--exp - (4) D, can be related tothe specific surface area S,,,,as follows: [ (_.__p)"] ratio of the total volume of fragments to the total surface. D,- _ (6) PSw where R(Dp) de,otes the mass fraction of the fragments smaller than the diameter D_, and Dc and n are the parameters of size and of devia[ion, respectively. For each The correlation between the specific surface area of th= experiment, the sieved particle size distribution was fitted debris and the peak pressure measured at the bottom of the by Rosin-Rammler's distribution function using a least- test capsule durin$ the experiments for the effect of fuel rod squares algorithm. In each experiment, the fraction of internal pressure Is shown in Fig. 11. The results indicate collected debris to the mass of fuel ranged from 70% to that higher peak pressure correlates with larger specific 98%. In obtaining the parameters D and n, it was surface area, that is, finer debris. Figure 12 shows the assumed that diameters of uncollected debris particles were correlation between the specific surface area of the debris smaller than 0.25 ram. Rosin-Rammler's distribution was and the thermal to mechanical energy conversion ratio. then applied tothe experimental data, including the masses When the specific surface area is more than 3000 mmZ/g, of particles having diameters below 4, 2, 1, 0.5 and 0.25 mm. Good applicability of Rosin-Rammler's function to the debris l_article size distribution is obtained in the Volume-Surface experiments/ The distribution parameter n ranged from MeanDiameter (mm) 0.22 to 1.17 in this study, When n becomes larger, Rosin- 1 0.1 0.01 50- Rammler's distribution approaches the lognormal _ , , distribution. For the case when n is three or higher, the a. Col_uleDiameter,, 72mm _1'• lognormal distribution should be used for the fitted _._ v function. Another possible fitted distribution is the upper 10 • ---- --- Pir J£ limit lognormal (ULLN) distribution(Fletcher, 1988). It o MP(I_, should be noted that the ULLN distribution needs three _ 5 zx a 0_ 07 ,9 o 0.I parameters concerning particles; maximum size, location o_ a -•-',--3.C and scale. Therefore, Rosin-Rammler's distribution was _. v _a "i-_.C [20 used in this study because of its simplicity and wide _ 1 v_.5.__,...__S applicability. _ 0.5" zx • 0.1 • _"5.'--'_ i 7."-(11o As an index for fragmentation, specific surface area S,_, _-"-_._ defined as the total surface area of the particles per unit 0.1 ........ ' ......... ' ........ mass, isderived by the integration of the fitted distribution 102 103 104 105 asfollows: Specific SurfaceArea (mm2/g) Sw-- , n--_____n_f Fig. 11 Peak pressure as a function of specific surface area pD, op._ [ of fuel debris x,[°( I"I Vo,umo- or,oce l-e _ "p.n_ MeanDiometer (mm) + L o. )j 1 0.1 0.01 "" 1 P _ _ CopsuleDiometer,,72mm Dp 0.5I ' ' _' • ' The geometric factor for fragmented debris particles, _, is ._o ___ assumed tobe six, which means particles are spherical and _ v" Pir !% dense. This assumption allows a conservative estimate of _c co • z_av_ _"OM.P""cq_-" the surface area to be derived from the debris particle size ,,, .& 0.1 o_ _"3.-"-iif" distribution. Porous debris has been observed in many _ _ '6-'"k-ff.1o20 steam explosion experiments. In this study, numerous ._ _ 0.05 "_ 5.-"6"i porous debris was also observed. However, the spherical, .t:_ ,_ %"O.--rT-- denseparticle assumption has been used for many studies u *"5.--TI10 because of the difficulty inestimating the particle geometry :_ - 8._ L__ factor. Therefore, although the absolute values of the 0.01 ........ ' ............ -:'_..-7_.. debris particle surface area are subject to uncertainty, it 102 103 104 105 may be of value to compare the data with this series of Specific SurfaceArea (mmZ/g) experiments As for D ,,,, the diameter when R(D) • p, P becomes 99.9% was adopte_. D.,,,_,=, 0.001 mm was also Fig. 12 Mechanical energy conversion ratio as a function of assumed. This value seemed [_ be realistic from the specific surface area 287 the conversion ratio isalso well correlated with the surface was not measured inthe experiment, it was ascertained in area. Therefore, the specific surface area of the fragmented the preliminary experiment that the average temperature fuel would serve as a good measure of the peak pressure estimated from the input energy under the adiabatic and conversion ratio, which inturn gives a good indication condition was almost equivalent to the temperature of the intensity of FCIs. measured bythe resistance method. Therefore, heat transfer from the rod surface to the ambient water is negligible in III. OUT-OF-PII,E EXPERIMENT comparison with the heat capacity of the heated rod. As the heat capacity of the stainless steel isabout 0.49 J/g.K, A. Experimental System the input energy density of 750 J/g'SS is roughly correspond to the temperature rise of 1530 K. The initial The loop used in the out-of-pile experiment is pressure andwatersubcoolingwerevariedfrom0.1 MPato illustrated in Fig. 13. A test vessel of 80 mm in inner 0.3 MPa and from 5 K to 110 K, respectively. The input diameter and 1000 mm in length is filled with stagnant energy density ranged from 650 J/g.SS to 950 J/g.SS. water. A small preheater at the bottom part of the vessel controls initial water temperature. The upper part of the In the out-of-pile experiment, the mechanical energy vessel isconnected toa separator by a glass pipe of 10mm is obtained as follows; in inner diameter and 500 mm in length. Inertia force of efflux water from the testvessel is mainly controlled bythe "* Ke°fo,(O-Po)Adt length of the glass tube. At the exit of the glass tube, a (7) small impact tube is installed to measure efflux velocity of 0 water. On both sides of the test vessel, windows are set to observe transient phenomena around the heated rod by a high speed camera. A piezo-electric type pressure where efflux velocity, v(t), is obtained by; transducer with the response time of less than 1 tas is t mounted on the wall of the vessel. A stainless steal rod f Pt(t)-P°d (8) watitthhedcieanmteerterofotfhe4vmesmsela.ndThleengrothd oisft1ra0n0siemnmtlyisheinastetadllebdy v(t) -- _ _ at large electric current produced by discharge from a power condenser bank of 2000 laF. The discharge time is about 4 ms. This value is almost equivalent to the width of Then the conversion ratio in the out-of-pile experiment is reactor power in the pulse irradiation of the NSRR. In the defined as a ratio of mechanical energy, K_,tototal energy out-of-pile experiment, the electric power input is shut input by the Joule heating. down when the rod isdispersed. Even in reactor transients the additional heat generation in dispersed fuels by fission B. Results and Discussion and disintegrations of fission products isnegligible after the loss of the fuel rod geometry. Therefore, the out-of-pile Pressure Generation The heated rod becomes molten with experiment canwell simulate boiling phenomena around the the input energy density of 650 J/g.SS or higher. A series dispersed melt. Though the temperature of the heated rod of photographs taken by the high speed camera and the corresponding pressure history are shown inFig. 14. In the ,.I. pressure plot, the history measured in the experiment with __-_ lower input energy density, resulting in non-melting of the Tank .- nucleate boilin_ stage, pressure peaks recorded in the I hexeapteerdimernotd, wisitlallsotheshhoiwghn ibnyputa ebnreorkgeyn dleinnes.ity,Dui.rein.gthea melting case, are less than 0.2 MPa, and notable difference n can not be seen incomparison with the non-melting case. Glass Tube However, pressure increases rapidly to ten times higher - value comparing with that of non-melting case when the _I_ _ bmn_,_ mheealtteindgroodccumrse.ltinWg,ithbotthhe nluarcgleeatienpuantdpofwilmer rbeosiulilntigngpeirniotdhse High-speed | _ t,w_ H,_ become very short (1 ms) and the temperature of the rod Camera rr-l'v'l'_['__ u-_ reaches tothe melting point for short time. Then, the upper T°O It !_ II eonfdheoaftitnhge,haenatdedanroedleicstrbicroksepnarkat 1is.4gmenseraaftteedr t(hPehointoitia(tbio)n). _ IIl_ q_IIl¢l J._I_ Heater_ "'%1 " 'UL.EJ ,_a Pressure reaches the maximum at 2.8 ms between photos _1"- "--l_j_ __ \Heatedrod (c) and (d)in the early stage of fragmentation and ' the electric current, the heated rod is deformed and broken a-L__'_ _ \-4.-m..m_XlOOmm datispbeortshionenodfsthaendmealttintgherodce.ntBery.theInhoothpessetresosbscearuvsaetidonbsy ---, Heater melting metal is ejected and dispersed like a water jet. It _ can be noted that the melting and the fragmentation process inthe early stage has an important role for generation of an _1_ intensive pressure peak. Peak Pressure Relations between the peak pressure and Fig. 13Out-of-pile experiment loop the input energy density in two different subcoolings are 288 (e) t=4,0 ms (r) t=50 ms (_) t=6.0 ms (h) t=6.6 ms miicooilg ( K ) O: 5.6 _- 9.4 I1: 5 7.9-,,6 4.0 ._12o_ _ :_ IJ/_ 10s 700 800 900 800 _ Fig. 15 Peak pressure versus input energy density I ______ 107: 0 ..... " - Time(ms) --, 13 Fig. 14 Photograph by high speed camera and the "" I _- "_ 0 0 corresponding pressure history a... shown in Fig. 15. The peak pressure increases i 106- monotonicallywith the increase of the input energy density up to 950 J/g.SS. The effect of water subcooling on maximum peak pressure are shown in Fig. 16. In the case of input energy density of 830 J/g.SS, maximum of the peak pressure appears at water subcooling of 25 K. The results indicate that there is the most suitable subcooling to generate the peak pressure. Input_ _: " sso (j/_) Mechanical Energy Conversion Ratio Figure 17 shows theexperimental resultof themechanical energyconversion ratio as a function of the input energy density. The 105 , I I I I I conversion ratio increased with the input energy density 0 50 100 150 both in the two different water subcoolingconditions. Maximum value of the conversion ratio obtained in the Lklula_ (K) experiment is approximately 0.01%. This value is considerably small in comparison with melt drop type Fig. 16 Peak pressure versus coolant subcooling experiments. One possible reason is that the pressure measured at the wall of the test vessel is not equal to that inversely proportional to square root of the distance from generated in the vapor film. If pressure propagates as a the cylindrical pressure source inthe heated rod to the wall. cylindrical acoustic wave, the measured pressure must be Here, rf and r,, are radii of the heated rod and the test multiplied by (r,,/rt)°_ = 4.5, because the pressure decays vessel, respectively. Considering this correction, maximum 289 10"2 1°3" ,!, - i i / . ... ,_ 102 I / I II I : 10 :" lubcoollng In_ oneriWdensity " " O: 9. 4 (K) 8 9 0 (Jig SUS) - At 8. 0 (i) 8 3 0 (J/I SUS) " /0 " 1-1: 7 . 0 (i) 7 5 0 (J/I SUS) / .- V: 8 3. 0 (i) 7 5 0 (Jll SUS) subcoo,ng (K) 1 I I , .I , I _ I , I i o: 5 6.-, 0 4 1 10 30 50 70 90 99 I : 5 7 . 9 --. 6 4 . 0 MuI friction of particles with smaller Ollimeter ( % ) 10 , i I ' I L Fig. 18 Debris particle size distribution obtained 700 800 900 in out-of-pile experiments Irnl_tenergy clenMty( JI g sus) g Fig. 17Mechanicalenergyconversion ratioversus input _F.,,,II i im_ i _ _ conversionenerrgaytiodeonbstaitiyned in the experiment becomes about ![ T'_1]_ ! _q i _ _' Debris Particle Size Distribution The size distribution of --_ .... Sit Al) the debris fragmented during the out-of-pile experiment is lO0tam inodia.m,e,ter toathettaoatal=mass rang,ed,,,3,0,%.s,to.7,0,%°,. . " ; Sill shown in Fig. 18. The mass ratio of particles with less than --,J]k_..-I.rVn_qT__'_.I__-- / -:-._ I _ dfriaffgicmucltntattoiond.iscussHowtheeveirn,flueitncecanofbetessteecnondthitaioinsthetolarthgee _..- t I l=-V,,x subcooling condition results in the production of finer V, i debris. Fig. 19 Conceptual description of surface stretch model IV. ANALYSIS A. Model 4) Superheated vapor in the vapor film follows to the ideal gas hiw During the melting and dispersion processes of the heated According to the observation by a high speed camera rod, two mechanisms can play a leading role with respect in the out-of-pile experiment, fragmentation process of the to enhancement of heat transfer. One is the increase of heated rod can be described as the following manner, heat transfer area due to the fragmentation, and the other is 1) Formation of thermal boundary layers in both solid decrease of thicknesses of thermal boundary layer and and liquid vapor film due to the stretch of surface. Schematics of 2) Incipient boiling and onset of nucleate boiling surface stretch model proposed in this study is shown in 1 TMraenltsinitgionandfrofmragnmuecnletaattieonboiolfingthetoheafltietd, brooilding Fig. 19. 5) Cooling of the dispersed particle The interfiice stretching rate S/S during fragmentation The model was formulated under the following can be described as fi)llows. The continuity equation is assumptions, described as; 1) One dimensional heat transfer m(_el 2) Film boiling directly follows the incipient boiling V. V = VII .V// + V • V, = 0 (9) since the duration of nucleate boiling is very short. 3) Interface between vapor and liquid is kept at the saturation temperature where, subscripts of//and I denote components of parallel 290 and normal directions to the surface. As describing in Fig. The effect of heat transfer due to surface stretch is 19,the stretching rate becomes; described by the second term of left hand side in this equation. In the proposed model including the surface (10) stretch concept, itisassumed that the cylindrical heated rod VII• V/! = --_ (;longates axially according to the surface stretch function, S(t)/S(0). Figure 20 illustrates the heat transfer model during the film boiling stage. The second order Then from Eq. (9), temperature profiles are assumed in the thermal boundary layers of the heated rod and liquid and in vapor film. V • V -- - -S (11) Then, the boundary layer integral method is applied. The S proposed model consists of; 1) Energy equations of the thermal boundary layers in As temperature gradient in the stretching direction is the heated rod and the liquid, negligible; 2) Mass and energy equations of vapor film during film boiling, VIIT= 0 (12) 3) Momentum equation of the efflux liquid, 4) State equation of the vapor and saturation condition at the vapor/liquid interface, then an energy balance equation isdescribed as follows; 5) Equations of mass and energy fluxes at the metal/vapor and vapor/liquid interfaces, + (13) ._ _ 6) iEnmcippiierinctalbociolirnrgel(aOtikounysamcao,nce1r9n8in6g), atnhde superheat of +(_.V) T V(_VT) pCp 7) Surface enhancement function. When Eq. (13) is integrated over thickness (5of thermal The details of the formulation are presented in Ref.(lnoue boundary layer or vapor film, the following equation is etal., 1992). To get the surface enhancement function S(t), obtained, it is necessary to know the dynamics of fragmentation. Though numerous possible mechanisms have been proposed - _ b in terms of fragmentation, pressure induced fragmentation a---r8 ] - fr [V ' ldr _-[v_r smeaenmys pmreossstureapppliuclasbelesoutorceths,e cbuorirleinngt satnudd/yorsicnocnedetnhsearteionar,e dt o o (14) around the melting rod. Several fragmentation models -- V (_VT) + 0 based on the boundary layer stripping, the Taylor instability pCv and the entrapment bythe micro jet have been investigated. However, they are applicable to fragmentation under larger pressure shock or pulse. Therefore, the surface where T is the averaged temperature across 8. When one enhancement function was derived from the following side of the boundary layer or the vapor film is fixed, consideration. It is assumed for the fragmentation process velocity of the other side become; that the melting metal which has initial surface area of AS(0) per unit length of the heated rod is successively V_.(8) = -8____S (15) divided by instability as described in Fig. 19. When an $ initial spherical particle with radius of Rmois divided successively into n panicles with radius of riafter i times Then, Eq. (14) becomes, division, a._.._+T[__ T(8)]S Rmo3 = nrl3 = n2r23 ..... n_r_3 (17) at s When the growth rate due to the surface instability can be -_5[VT(8) - _T(0)] + 0 (16) assumed as a constant c, the fragmentation time, Ati, of pCp particle with radius of r__1can be described as follows; At_ - r_-I - Kom.- n-O-l)/3 (18) '[L When the average radius of particle becomes rb after k times division, the fragmentation time "tt,becomes, l • AtRm°(1-n-k/3 ) Rm°-rb (19) TESTPIECE k Rm _ X _ andtime needed for itimes division, tiis, ,ESrsEerlo, ti = l-n -'/3} c (1-n-'rJ) Fig. 20 Heat transfer model around heated rod 291 From Eqs.(19) and (20), in the experiment. However, the analysis with the larger surface enhancement function results in generation of the rt = r(Q = Rmon-irJ = R_(1 - RR",o°-xrbbt _IJ (21) dheignhsietry,pressusrufraec.e Tehnehatnracnesmieenntt hirsattoer,iesproesfstuhree inapnudt eenfefrlguyx velocity in the analysis are illustrated in Fig. 22. The number of particles n(t0 attime ti(s) becomes from Eq. Peak Pressure and Mechanical Energy Figure 23 shows (17), the analytical and experimental results of the peak pressure as a function of the input energy density. Although the n(t,)=n' =/,x/_.o/3 (22) analysis predicts higher peak pressure than the experimental _r(Q) data, the dependency on the input energy density is well described bythe analysis. Relation between the mechanical and total surface area, S(ti) at tiis, _ 20 fc,r O<t,<% x 0 107g s(o)=AS(O)L=,,4.RJ L,, (24) lOB where I_n, and R_ are described in Fig. 20 and R_, rband >- %are the initial radius of heated rod, final radius of the _ 102 fragmented particles and the fragmentation time, _ I0_ %are set at 50 tamand 3 ms from the post test examination 1 roenspdeecbtirvise.ly.ThTeheseftinoafl reaqduiautsionr_sanids tshoelvferdagnmuemnteartiicoanllytimbey i .01t J t_ v¢ 3 830(J/O) >, B. Numerical Results and Comparison with _ 8o(K) 2 experimental data o.1(m,) the Runge-Kutta scheme with variable time mesh..,_'_ 100 i "1 Pressure Trace The numerically predicted pressure history a(m,) t 6. is compared with the experimental data in Fig. 21. The = 0 first small peak isgenerated by the transient boiling art,und 0 [5 10 15 the pre-melting heated rod and the second large peak is Time(ms) caused in the period of melting and fragmentation of the heated rod. Since the relatively small surface enhancement Fig. 22 Transient histories of parameters in the analysis function is used in this calculation in order to have good agreement with respect to maximum pressure, the pressure peak of the analysis appears much later than that recorded 107 Analysis 6 , , , I i \ _ InpuetneqW.dmet:y830,l/l; 3- I \ "_:so_._ ca- _ Experiment -1 13_ •-2 i i l I w 105 , i , I i i , i j -5 o s 1o 15 20 25 500 600 700 800 900 1000 _,mt_=) Inputenergy density (J/g) Fig. 21 Pressure histories during transient Fig. 23 Peak pressure versus input energy density 292 energy and the input energy in the conditions of water propagation. In the analysis, maximum conversion ratio subcooling of 60 K and initial pressure of 0.1 MPa is becomes near 0.1%. shown in Fig. 24. The analytical result of the mechanical energ shows the similar trend as the experimental data, Parameter sensitivity Sensitivities of the water but the calculated mechanical energy is about ten times subcooling, fragmentation time and particle size to peak higher than the experimental data. As it can be seen in pressure and mechanical energy generation are examined in pressure histories in Fig. 21, time span of the second peak the analysis. Each effect is shown in Fig. 26(a), (b) and m the analytical result is much wider than the peak (c), respectively. Inthe analysis, the superheat temperature recorded inthe experiment. Inthe analysis, it is assumed of the transition to film boiling increases with the water that the whole heated rod is melt and fragmented at same subcooling. Then the larger subcooling results in the time. On the other hand, the peak pressure appears in the increased heat flux from the melt to the water and in the experiment when the both ends and the center of the heater higher pressure peak. On the other hand, the duration time rod are melt and fragmented, as shown in Fig. 14. This of the pressure generation decreases inthe large subcooling difference could result in the relatively large discrepancy condition due to the large condensation rate of steam. The between the analysis and the experiment. As shown inFig. mechanical energy is derived from the integration of the 25, the conversion ratio shows the same trend as the pressure with respect to time, so the larger subcooling mechanical energy. As noted previously, maximum value results in the lower mechanical energy. The decreases of of the conversion ratio obtained in the experiment is the fragmentation time and particle size cause the higher approximately 0.01%, and it becomes about 0.045% by pressure and the larger mechanical energy. employing the correction concerning pressure decay during .,"_.---_.. 10 _ _,_ 10-1 ._,_/ o_ ....-. o Anolysis _- 1 ..... Analysis .- c: 0 _ a c 10-2 o o Experimen_ ,__ t_ "_ °10 -1 o > o o .c:o Experiment c 0 I"1 Q 10-2 , t , I i I , , , 10-3 , i , I , = , = , 500 600 700 800 900 1000 500 600 700 800 900 1000 Input energy density (J/g) Input energy density (J/g) Fig. 24 Mechanical energy versus input energy density Fig. 25 Mechanical energy conversion ratio as a function of input energy density 107 10 101 .10 10=t:: " I i_ , ix_.u:euaro*tv:eo.,(--) ,_lOz_l <-- _, :3(m,) INi" 10 ' 10I_ 1 100 50 100 0 5 10 0 50 100 (a) Liquidiubcooling (K) (b) Fragmentationtime (ms) (C) Fragmentedparticleradius(yam) Fig. 26 Sensitivities of coolant subcooling, fragmentation time and fragmented debris radius on mechanical energy 293 V. SUMMARY Though the analysis describes the peak pressure, it has considerable discrepancy with the experimental The generation of destructive forces during FCIs in a data concerning mechanical energy. Further severe RIA was demonstrated through the in-pile improvement of the model is needed. experiments with a LWR uranium dioxide fuel. Transient behavior of the rod during a severe power transient was NOMENCLATURE also investigated inthe out-of-pile experiment bythe Joule heating of a stainless steal rod. The analytical model A = ttorizontal cross-section area of the out-of-pile including surface stretch during melting and fragmentation test vessel (m2) was developed, and its applicability to the out-of-pile c -- Factor for unit justification experiment was discussed. Cp = heat capacity at constant pressure (J/g'K) D_ = Size parameter of the Rosin-Rammler's The effects of the energy deposition, coolant conditions distribution (mm) and fuel rod internal pressure on the _eneration of Dp = Diameter of the fragmented fuel debris (ram) destructive forces were extensively investigated in the Dp,m,x Maximum particle diameter for the integration of NSRR experiments. The results are summarized as follows: the fitted distribution (mm) (a) For non-pressurized fresh fuel rods, threshold Dp.m_,,= Minimum particle diameter for the integration of enthalpy for the initiation of FCIs is about 1.4 the fitted distrit:ution (mm) kJ/g.UO v Breach of the cladding and resultant D, = Volume-surface mean diameter (mm) ejection of molten fuel into the coolant seems to be K, - Mechanical energy generated by FCIs (J) major mechanism for this condition. _ = Length of glass tube (m) (b) The increase of hydrogen generation due to the mf = Mass of fuel (g) occurrence of fuel fragmentation can be observed, rrk,, = Mass of water slug (kg) but this effect is not vigorous. It is thought that the n = Distribution parameter of Rosin-Rammler's most of hydrogen is generated from cladding distribution oxidation. Pt = Pressure in the out-of-pile test vessel (Pa) (c) Decreasing the coolant subcooling reduces the P0 = Pressure in mechanical energy conversion ratio but this effect is Po, = Pressure of the capsule plenum gas (Pa) not important for large energy depositions of around Ps,,,o = Initial pressure of the capsule plenum gas (Pa) 2.0 kJ/g.UO2. Pg,,._ = Peak pressure of the capsule plenum gas (Pa) (d) The mechanical energy conversion ratio decreases Pin = Initial internal pressure of the fuel rod (MPa) when the water/fuel ratio is decreased, possibly Q = Deposited energy per unit mass of UO2 fuel because of the reduced mixing length of molten fuel (kJ/g) jet in the coolant. (_ -- Input power density in the out-of-pile (e) Intense pressure waves, which had a peak pressures experiment (W/m3) higher than 24 MPa, are measured in experiments rb = Radius of fragmented particles (m) with highly pressurized fuel rods. It isexpected that rf = Radius of the heated rod in the out-of-pile a hydrodynamic effect results inenhanced mixing of experiment (mm) the molten fuel with the coolant, rw = Radius of the test vessel in the out-of-pile (f) The effect of the fuel rod internal pressure is more experiment (mm) apparent in experiments with fuel enriched to 10% R(Dp) = Rosin-Rammler's distribution function of the than in experiments with 20% enriched fuel. An mass below a given size intensi';e FCI can be expected in the case of Rmo = Initial equivalent radius of melting metal (m) irradiated fuel rods in a commercial reactor, which S = Surface area in interface (m2) will have a lower enrichment and increased pressure Sw = Specific surface area of the fragmented fuel due to the accumulation of the gaseous fission debris (mm2) products. T = Temperature (K) (g) The intensity of the destructive forces are well u = Velocity of water slug (m/s) correlated with the specific surface area of debris by Vo,0 = Initial volume of capsule plenum gas (nl3) using Rosin-Rammler's fitted distribution. The Vs_,'_ Volum.e...of capsule plenum gas at Ps,s=Psas,l(m3) specific surface area of the fragmented fuel would Vj.' Velocity vector of vertical dlrectmn to surface serve as a good measure of the peak pressure and (m/s) conversion ratio, which in turn gives a good VH = Velocity vector of parallel direction to indication of the intensity of FCIs. surface(m/s) The simultaneous acquisition of visual appearance of 6 = Thickness of boundary layer or vapor film (m/s) melting and dispersion of the heated rod end transient _ = Fuel enrichment (%) pressure history was realized inthe out-of-pile experiment. TI = Thermal to mechanical energy conversion ratio The results obtained in the out-of-pile experiment and the (%) analysis are summarized as follows; i< - Thermal diffusivity coefficient (m2/s) (h) The increase of the input energy results in the Kg = Specific heat ratio of capsule plenum gas generation of the higher pressure peak and the larger 13 = Density (kg/m3) mechanical energy. 13f = Density of the fragmented fuel debris (g/ram3) (i) There is the most suitable coolant subcooling to 13t Liquid density (kg/m3) generate the higher peak pressure. % = Fragmentation time (s) (j) An analytical model considering surface stretch _ = Geometry factor of the fragmented fuel debris during melting and fragmentation was proposed. 294 REFERENCES Fletcher, D. F., (1988) "The Particle Size Distribution of Solidified Melt Debris from Molten Fuel-Coolant Interaction Experiment", Nuclear Engineering and Design., 105, 313-319. Fu,jishiro, T. anti Fuketa, T., (1989) "NSRR Experimental Results on Fuel/Coolant Interaction during a Severe Reactivity Initiated Accident", Proc. 4th Int. Topical Meeting on Nuclear Reactor Thermal- Hydraulics(NURETH-4), Karlsruhe, Germany, October 10- 13, 1992, Vol.1, 297-303. Fuketa, T. and Fujishiro, T., (1992) "Generation of Dcstmctivc Forces During Fucl/Coolant Interactions Undcr Scvcrc Reactivity Initiated Accident Conditions", Proc. 5th Int. Topical Meeting on Nuclear Reactor Thcrmal- Hydraulics(NURETH-5), Salt Lakc City, Utah, Scptcmbcr 21-24, 1992, Vol.3, 753-761. Inabe, T. and Fuketa, T., (1992) "Hydrogen Generation Measurement Tests", Annual Progress Report onthe NSRR Experiments 20, Reactivity Accident Research Laboratory and NSRR Operation Division, Japan Atomic Energy Research Institute, JAERI-M 92-049, 35-37. (in Japanese) Ino.qe, A., Shinano, M. and Hirabayashi T.,(1991) "Fundamental Study cn Thermo-Hydraulic Behaviors of a Fucl Channcl during a Scvcrc Powcr Transicnt", Proc. 1st JSME/ASME Joint Int. Conf. Nuclear Engineering(ICONE- 1), Tokyo, Japan, November 4-7, 1991, Vol.2, 227-233. Inoue, A., Aritomi, M., Takahashi, M. and Shinano, M._ (1992) "Expcrimental and Analytical Study on Vapor Explosion of Melting Heated Rod During A Severe Power Transient", Proc. 5th Int. Topical Mccting on Nuclcar Reactor Thermal-Hydraulics (NURETH-5), SaltLake City, Utah, September, 21-24, 1992, Vol.3, 762-771. Okuyama, K., (1986) "Study on Transient Boiling Phenomena and Enhancement of Critical Heat Flux during Very High Heat Generation", Ph.D Thesis, Tokyo Institute of Technology. Tsuruta, T., Ochlai, M. and Saito, S., (1985) "Fuel FragmentationandMechanical Energy Conversion Ratio at RapidDeposition of High Energy in LWR Fuels", Journal of Nuclear Science and Technology, 22-9, 742-754. Vaughan, G. J. (1979) "Some Theoretical Considerations Concerning Molten Fuel-Coolant Interaction Debris Size", 4th CSNI Specialist Meeting on Fuel-Coolant Interaction inNuclear Reactor Safety, Bournemouth, April 2-5, 1979. 295