NASA Technical Reports Server (NTRS) 20130013387: On the Statistical Analysis of X-ray Polarization Measurements PDF
Preview NASA Technical Reports Server (NTRS) 20130013387: On the Statistical Analysis of X-ray Polarization Measurements
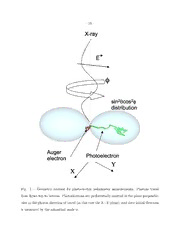
On the Statistical Analysis of X-ray Polarization Measurements T. E. Strohmayer and T. R. Kallman X-ray Astrophysics Lab, Astrophysics Science Division, NASA’s Goddard Space Flight Center, Greenbelt, MD 20771 Received ; accepted – 2 – ABSTRACT In many polarimetry applications, including observations in the X-ray band, the measurement of a polarization signal can be reduced to the detection and quantification of a deviation from uniformity of a distribution of measured an- gles of the form A + Bcos2(ϕ (cid:0) ϕ ) (0 < ϕ < π). We explore the statistics 0 of such polarization measurements using both Monte Carlo simulations as well as analytic calculations based on the appropriate probability distributions. We derive relations for the number of counts required to reach a given detection level (parameterized by β the “number of σ′s” of the measurement) appropriate for measuring the modulation amplitude a by itself (single interesting parameter case) or jointly with the position angle ϕ (two interesting parameters case). We show that for the former case when the intrinsic amplitude is equal to the well known minimum detectable polarization (MDP) it is, on average, detected at the 3σ level. For the latter case, when one requires a joint measurement at the same confidence level, then more counts are needed, by a factor of (cid:25) 2.2, than that required to achieve the MDP level. We find that the position angle uncertainty at 1σ confidence is well described by the relation σ = 28.5(degrees)/β. ϕ Subject headings: polarimetry: general|statisticalanalysis: MonteCarlosimulations – 3 – 1. Introduction Emission and scattering processes thought to be important in many astrophysical X-ray sources are likely to impart specific polarization signatures, but to date there have only been a few positive detections of polarization from cosmic X-ray sources, largely due to sensitivity limitations. Some of the earliest and highest precision measurements were made with the OSO-8 Bragg reflection polarimeter (Kestenbaum et al. 1976; Weisskopf et al. 1976), and include high significance measurements of the linear polarization properties of the Crab nebula in several energy bands (Weisskopf et al. 1978). More recently, observations with the INTEGRAL spectrometer SPI and imager IBIS have exploited the polarization dependence of Compton scattering to infer the linear polarization properties of the Crab at γ-ray energies (Dean et al. 2008; Forot et al. 2009). These results indicate that the > 200 keV flux from the Crab nebula is highly polarized ((cid:25) 50%), with a position angle consistent with the pulsar rotation axis. In the last few years the development of micropattern gas detectors has enabled the capability to directly image the charge tracks produced by photoelectrons, thus enabling use of photoelectric absorption in a detection gas as a direct probe of X-ray polarization (Costa et al. 2001; Black et al. 2004; 2010). It is likely that such technology will be employed in the not-too-distant future to sensitively explore the polarization properties of many classes of astrophysical X-ray sources for the first time. In this paper we explore the question of how one detects, measures, and characterizes a polarization signal with a photoelectric polarimeter. The remainder of this paper is organized as follows; in x2 we outline the basic problem of detecting a modulation in a distribution of angles, and we describe the angle distributions used throughout the paper. In x3 we briefly outline the probability distribution relevant to such polarization measurements. In x4 we describe our Monte Carlo simulations and present our results. We – 4 – conclude with a short summary in x5. 2. Statement of the Problem The angular distribution of photoelectrons ejected by a linearly polarized beam of photons (X-rays) is proportional to sin2(θ)cos2(ϕ)/(1(cid:0)βcos(θ))4 (see, for example, Costa et al. 2001), where θ is the emission angle measured from the direction of the incident photon (0 < θ < π), and ϕ is the azimuthal angle measured relative to the polarization vector of the incident photon (see Figure 1 for the basic geometry applicable to a photoelectric polarimeter). In most practical situations the angle θ is not inferred directly, but the electron charge track projected into the plane orthogonal to the direction of the photon (the plane defined by θ = 90 deg) is imaged and thus ϕ can be estimated for each detected photon. The angle ϕ is measured around the line of sight to the target of interest and can be referenced to, for example, local North on the sky. The presence of a significant linear polarization component is then evident in the distribution of azimuthal angles. For example, an unpolarized photon flux will produce a uniform distribution in the angle ϕ, whereas a linear polarization component produces a distribution peaked at a particular azimuthal angle, ϕ . 0 In general, the observed distribution in ϕ will be of the form, S(ϕ) = A+Bcos2(ϕ(cid:0)ϕ ). (1) 0 This distribution has an amplitude of modulation given by, a (cid:17) (S (cid:0) S )/(S + max min max S ) = B/(2A + B), and a position angle (the angle at which the distribution has a min maximum) given by ϕ , thus, the detection of polarization can be reduced to a statistical 0 detection of a modulation in the distribution of angles, ϕ. Such a distribution is often referred to as a modulation curve. – 5 – In principle the angle ϕ can be measured in the range from 0(cid:0)2π (0 - 360 degrees), however, due to the two-fold symmetry of the cos2(ϕ) dependence of the angular distribution of ejected photoelectrons, it is sufficient to consider distributions over a range of angles from 0 to π (0 - 180 degrees). An equivalent and often convenient way to express this distribution is using the so-called Stokes decomposition, S(ϕ) = I +Qsin(2ϕ)+U cos(2ϕ), (2) where I, Q and U are the well-known Stokes parameters, the modulation is now given by a = (Q2 +U2)1/2/I, and the position angle is ϕ = 1/2tan−1(Q/U). 0 Now, the amplitude of modulation a is not in general equal to the source polarization amplitude, a , because a detector is not a perfect analyzer and will not provide an exact p measurement of the true photoelectron angle ϕ. That is, individual angle estimates will have some uncertainty associated with them and these will produce a uniform (unmodulated) component to the measured distribution even in the case of a 100% polarized beam. This “lossiness” of the angle estimates is quantified in terms of the so-called detector modulation, µ, which is the modulation amplitude produced in the detector by a 100% polarized X-ray beam. In general, µ can depend on a number of factors, including the energy of the incident photons, and the composition and pressure of the absorbing gas, among others (see Paciani et al. 2003, Bellazini et al. 2003). In the absence of background, the amplitude of polarization is just a = a/µ. In general, a is larger than the measured amplitude of p p modulation, a, because as noted above, detectors are not 100% efficient, and some of the intrinsic polarization amplitude is smeared out. – 6 – 3. Probability Distribution Previous studies have shown that the joint probability distribution for a measurement of polarization amplitude, a, and position angle, ϕ is given by ( ) Na N P(N,a,a ,ϕ,ϕ ) = exp (cid:0) (a2 +a2 (cid:0)2aa cos2((ϕ(cid:0)ϕ ))) , (3) 0 0 4π 4 0 0 0 where a, a , ϕ, ϕ , and N are the measured amplitude, the true amplitude, the measured 0 0 position angle, the true position angle, and the number of detected photons, respectively (see, for example, Weisskopf, Elsner & O’Dell 2010). In the case of no intrinsic polarization, a = 0, the distribution simplifies substantially to 0 ( ) Na N P(N,a) = exp (cid:0) a2 , (4) 4π 4 and this expression can be readily integrated to find the probability of measuring an amplitude, a, if there is no intrinsic polarization. The amplitude that has a 1% chance of being measured is referred to as the minimum detectable amplitude (MDA), and it is p relatively straightforward to show that MDA = 4.29/ N. The polarization amplitude that would produce this modulation amplitude in a particular detector system is called the minimum detectable polarization (MDP), and based on the discussion above is just p MDP = MDA/µ = 4.29/(µ N). Furthermore, if we are not concerned with the position angle, ϕ, then we can integrate equation (3) over angles and obtain the distribution, ∫ π/2 a (a2 +a2) aa P(N,a,a ) = P(a,ϕ)dϕ = exp((cid:0) 0 )I ( 0) (5) 0 σ2 2σ2 0 σ2 −π/2 where I is the modified Bessel function of order zero, and σ2 = 2/N. This distribution is 0 known as the Rice distribution (Rice 1945) and it reflects the fact that the amplitude is always a positive quantity, and so the distribution must go to zero for a = 0. An important property of this distribution concerns the second moment, which is related to the width, – 7 – and is given by: < a2 >= a2 +4/N which shows that the distribution width increases with 0 a . 0 4. Monte Carlo Simulations Without loss of generality an X-ray source’s linear polarization characteristics can be described by the modulation amplitude, a , and position angle, ϕ (in the range from 0 - 0 0 π), that would be produced in a particular detector system. In making an observation a total of N photons are observed for each of which an angle ϕ is estimated for the ejected i photoelectron in the range from 0(cid:0)π (0 - 180 deg). One can then create a histogram of the number of events (photons) in each of M position angle bins, where the bin size (in degrees) is ∆ϕ = 180/M. One can then do least-squares (χ2) fitting to estimate both a, ϕ, and their 1σ uncertainties (in practice we fit the modulation curves with the Stokes form of the distribution, equation 2). We call this a measurement of polarization. In effect, what is measured is the modulation amplitude, a, and it is the knowledge of the detector system, expressed in terms of µ, that enables this to be converted to a source polarization amplitude via the expression a = a/µ. p This procedure is quite amenable to simulation with Monte Carlo techniques, and here we present results of such simulations, both in the case with a = 0 and a > 0. For now we 0 0 ignore background considerations and work only in terms of modulation amplitudes, that is, the following results can be considered applicable to any detector system, regardless of the µ value that characterizes its polarization sensitivity. The simulations proceed as follows, for a given set of true parameter values, a and ϕ , 0 0 we compute a number, M , of simulated data sets each of which has N photons. For each sim simulated data set we bin the resulting angles to form a modulation curve and for each the – 8 – Stokes form of the distribution (equation 2) is fitted to determine best-fit values for Q, U, and I, and their 1σ uncertainties, σ , σ , and σ , respectively. We can use the fitted Stokes Q U I parameters to express the results in terms of a and ϕ using the expressions defined above. The 1σ uncertainties, σ and σ , can also be determined by standard error propagation a ϕ methods, which yields, ( ) σ = a (σ /I)2 +(σ2/(Q2 +U2)) 1/2, (6) a I Q and (√ )( ) σ (deg) = (180/π) (x2)/(2(1+x2)) (σ /Q)2 +(σ /U)2 1/2, (7) ϕ Q U where, x = Q/U , and σ , σ , and σ are the standard 1σ uncertainties on the fitted I Q U quantities, I, Q and U. The procedure can then be repeated with different values of N. All the Monte Carlo simulations described here were done using IDL, and uniform deviates were obtained with IDL’s random number generator randomu. We use a least-squares fitting routine within IDL developed by Craig Markwardt that is based on MINPACK-1 (see http://cow.physics.wisc.edu/˜craigm/idl/fitting.html). In all of the least squares fits all parameters are allowed to vary. 4.1. Results with a = 0: Minimum Detectable Amplitude (MDA) 0 In the case of a = 0 the distribution of angles, ϕ, is uniform, which can be easily 0 simulated with a random number generator that produces uniform deviates. We obtain from this procedure a distribution of best-fit amplitudes, a, from which we can estimate the value a that has a 1% chance probability of being measured. This is just the familiar 1% MDA described above. Figure 2 shows a comparison of the results from the simulations p (blue square symbols) versus the analytic expression given above, 4.29/ N (solid line). We computed M = 10,000 simulations for these results, and we used 16 position angle sim – 9 – bins for the modulation curves. Figure 2 shows that the a = 0 simulations are in good 0 agreement with the analytic result, giving us confidence that our simulation procedures are correct. 4.2. Results with a > 0: Detection of Polarization 0 We can now explore a number of issues with regard to detection of polarization. For example, how many counts are needed to measure a modulation amplitude to a particular precision, and for a given precision in the amplitude measurement, how accurately can the position angle be measured? To address these questions we perform additional simulations using true distributions with specified amplitudes and position angles. For the illustrative examples below we used two different amplitudes, both with ϕ = 0, however, we have explored many different 0 cases and all the results summarized here are independent of the particular values of a or 0 ϕ used. The example distributions described below are; S(ϕ) = 10 + 1cos2(ϕ (cid:0) 0) and 0 S(ϕ) = 10+2cos2(ϕ(cid:0)0). These examples correspond to intrinsic modulation amplitudes, a , of 1/21 and 2/22, respectively. For a specific detector these would correspond to 0 polarization amplitudes, a = 1/(21µ), and 2/(22µ). p To determine the number of counts, N, needed to reach a polarization sensitivity given p p by the MDP value we require that MDP = 4.29/µ N = a = a/µ, and thus a = 4.29/ N. p Note that here µ cancels out, and to achieve MDP values at these amplitudes requires (212)(cid:3)4.292 = 8116.21, and (22/2)2 (cid:3)(4.29)2 = 2226.90 counts, respectively. Note that this may seem a trivial point, but it’s important to keep the terminology as precise as possible. Below we will compare the counts needed to reach a certain MDP, N , and the counts mdp needed to measure the same amplitude of polarization to a certain precision, N. While N – 10 – and N will individually depend on µ, the ratio, N/N , cannot depend on µ, that is, it mdp mdp is independent of the detector system employed. When a > 0 we sample random angles from the true distributions by the so-called 0 transformation method. We first compute the cumulative distribution of S(ϕ), then draw uniform deviates, x, and find the corresponding value of ϕ(x) in the cumulative distribution. We use the root finder ZBRENT implemented in IDL to solve for ϕ given x. We can thus draw a specific number of events, N, from the true distribution. For each value of N we compute a large number M of realizations, to each of which is fitted the Stokes sim distribution to determine the best fit values of I, Q, and U (and thus a and ϕ), and their 1σ uncertainties. We can thus simulate the distributions of a and ϕ for different N. 4.3. Single Parameter Con(cid:12)dence Regions Here we present the results of our simulations in several ways. First, we used the results from M = 1,000 realizations for different values of N to find the mean values of a, and ϕ sim and their 68% confidence ranges. These are derived for each parameter independently of the other, that is, they are 1-dimensional (single parameter) ranges. For example, if one were interested in asking the question, is a source (or population of sources) polarized, without regard to the particular position angle of the electric vector, then the 1-d distribution would be appropriate. We explore the joint, 2-dimensional distributions below in x4.4. Figure 3 shows an example simulated distribution of measured amplitudes, a, computed with N = 20,000 events and a = 2/22 (with ϕ = 0). The left panel shows the differential 0 0 (binned) distribution, and the right panel shows the same results expressed as a cumulative distribution. We also computed similar distributions for the measured position angle, ϕ. Procedurally we use the estimated cumulative distributions to identify the mean of
