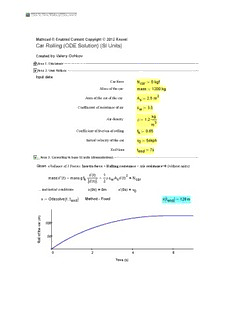
CClliicckk ttoo VViieeww MMaatthhccaadd DDooccuummeenntt Mathcad ® Enabled Content Copyright © 2012 Knovel Car Rolling (ODE Solution) (SI Units) Created by Valery Ochkov Area 1: Disclaimer Area 2: User Notices Input data Car force N (cid:29)(cid:32) 0 kgf car Mass of the car mass(cid:29)(cid:32) 1200 kg 2 Area of the cut of the car A (cid:29)(cid:32) 2.5 m s Coefficient of resistance of air c (cid:29)(cid:32) 3.5 w kg Air density (cid:1)(cid:29)(cid:32) 1.2 3 m Coefficient of friction of rolling f (cid:29)(cid:32) 0.65 k Initial velocity of the car v (cid:29)(cid:32) 54kph 0 End time t (cid:29)(cid:32) 7s end Area 3: Converting to base SI units (dimensionless) Given a balance of 3 Forces: Inertia force + Rolling resistance + Air resistance=0 (without units) x'(t) 1 2 massx''(t) (cid:14) massgfk (cid:14) (cid:1)cwAsx'(t) = Ncar x'(t) 2 ... and initial conditions x(0s) = 0m x'(0s) = v 0 (cid:11) (cid:12) (cid:11) (cid:12) x(cid:29)(cid:32) Odesolve t(cid:15)(cid:3)t Method - Fixed x t (cid:32) 126m end end m) ( r 100 a c e h of t 50 oll R 0 2 4 6 Time (s) Click to View Mathcad Document Mathcad ® Enabled Content Copyright © 2012 Knovel Car Rolling (ODE Solution) (US Units) Created by Valery Ochkov Area 1: Disclaimer Area 2: User Notices Input data Car force N (cid:29)(cid:32) 0 lbf car Mass of the car mass(cid:29)(cid:32) 2600 lb 2 Area of the cut of the car A (cid:29)(cid:32) 26.91 ft s Coefficient of resistance of air c (cid:29)(cid:32) 0.35 w lb Air density (cid:1)(cid:29)(cid:32) 0.0749 3 ft Coefficient of friction of rolling f (cid:29)(cid:32) 0.25 k Initial velocity of the car v (cid:29)(cid:32) 35 mph 0 End time t (cid:29)(cid:32) 7s end Area 3: Converting to base SI units (dimensionless) Given a balance of 3 Forces: Inertia force + Rolling resistance + Air resistance=0 (without units) x'(t) 1 2 massx''(t) (cid:14) massgfk (cid:14) (cid:1)cwAsx'(t) = Ncar x'(t) 2 ... and initial conditions x(0s) = 0ft x'(0) = v 0 (cid:11) (cid:12) (cid:11) (cid:12) x(cid:29)(cid:32) Odesolve t(cid:15)(cid:3)t Method - Fixed x t (cid:32) 75ft end end (ft) 60 r a c he 40 of t oll 20 R 0 2 4 6 Time (s) Click to View Mathcad Document Mathcad ® Enabled Content Copyright © 2012 Knovel Finding a Root of Equation x=f(x) by the Simple Iterations Method Created by Valery Ochkov Area 1: Disclaimer Area 2: User Notices Function of one argument - the right part of the equation x= f(x), where you want to find a root (the value of the x at which the equation x= f(x) becomes an identity) 2.1 f(x)(cid:29)(cid:32) (cid:16)0.2(cid:152)x (cid:14) x(cid:14) 2 Range of Plot x (cid:29)(cid:32) 2.7 x (cid:29)(cid:32) 3.2 1 2 Guess Value x(cid:29)(cid:32) 2.8 You can change the value of the variable iteration and see on the plot the approximation to the root of the equation x = f(x) iteration (cid:29)(cid:32) Area 3: Solution (cid:11) (cid:12) Iterations xi = f xi(cid:16)1 xx1 3.1 3 yy1 2.9 2.8 2.7 2.7 2.8 2.9 3 3.1 x f(x) Points of Iterations Tolerance T (cid:11) (cid:16)3 (cid:16)3 (cid:16)3(cid:12) (x(cid:16) f(x)) (cid:32) (cid:16)0.262 0.097 (cid:16)0.04 0.016 (cid:16)6.474(cid:117) 10 2.605(cid:117) 10 (cid:16)1.05(cid:117) 10 Iterations to the root T x (cid:32) (2.8 3.062 2.965 3.005 2.989 2.995 2.993) Click to View Mathcad Document Mathcad ® Enabled Content Copyright © 2012 Knovel Newton Method for Zero Finding of the Function y(x) Problem. To find in the section [a, b] unique zero (root) of function y (x) Created by Valery Ochkov Area 1: Disclaimer Area 2: User Notices 3 2 Function y(x)(cid:29)(cid:32) x (cid:16) 5x (cid:16) 4.5 Range of Plot x1(cid:29)(cid:32) (cid:16)2.5 x2(cid:29)(cid:32) 5.5 y1(cid:29)(cid:32) (cid:16)35 y2(cid:29)(cid:32) 15 First x x(cid:29)(cid:32) (cid:16)2 iteration (cid:29)(cid:32) Area 3: Method Area 4: Solution x x 1 10 (cid:16)2 0 2 4 (cid:16)10 (cid:16)20 (cid:16)30 (cid:167) "n =" 0 1 2 3 4 5 (cid:183) (cid:168) (cid:184) (cid:168) "x =" (cid:16)2 (cid:16)0.98437 (cid:16)0.17667 2.32909 (cid:16)0.37706 0.87726 (cid:184) Iterations(cid:32) (cid:168) (cid:184) "y(x) =" (cid:16)32.5 (cid:16)10.29882 (cid:16)4.66158 (cid:16)18.9888 (cid:16)5.26446 (cid:16)7.67281 (cid:168) (cid:184) (cid:169)"error =" 0 (cid:16)1.01563 (cid:16)0.8077 (cid:16)2.50576 2.70615 (cid:16)1.25432(cid:185) Click to View Mathcad Document Mathcad ® Enabled Content Copyright © 2012 Knovel Secant Method of Zero (Root) Finding of the Function y(x) Created by Valery Ochkov Area 1: Disclaimer Area 2: User Notices Function of one argument, where you want to find a zero (the value of the argument in which the function ravnv zero) 3 2 y(x)(cid:29)(cid:32) x (cid:16) 5x (cid:16) 4.5 Range of Plot x1(cid:29)(cid:32) (cid:16)2.5 x2(cid:29)(cid:32) 5.5 y1(cid:29)(cid:32) (cid:16)35 y2(cid:29)(cid:32) 15 First x x (cid:29)(cid:32) 2.8 1 You can change the value of the variable iteration and see on the plot the approximation to the zero function y(x) iteration (cid:29)(cid:32) Area 3: Method Area 3: Solution 10 (cid:16)2 0 2 4 (cid:16)10 (cid:16)20 (cid:16)30 (cid:11) (cid:12) x (cid:32) 2.8 x (cid:32) 2.801 x (cid:32) (cid:16)2.058 y x (cid:32) (cid:16)34.398 1 2 3 3 Click to View Mathcad Document Mathcad ® Enabled Content Copyright © 2012 Knovel Steiner Point Problem. You need to design takings from the electric cable to two points (to two houses) so that the total length of takings was minimal. You can change the coordinates of two points of the branches (from 0 to 100), and see the circuit branches, as well as the coordinates of the possible tee. Created by Valery Ochkov Area 1: Disclaimer Area 2: User Notices coordinates 1-st point coordinates 2-d point x1(cid:29)(cid:32) 0 y1 (cid:29)(cid:32) x2 (cid:29)(cid:32) y2 (cid:29)(cid:32) Area3:Method Area 4: Solution of the Task 110 100 90 80 70 60 50 40 30 20 10 electric cable (cid:16)10 0 10 20 30 40 50 60 70 80 90 100 110 (cid:16)10 (cid:167)27.679(cid:183) Steiner Point(cid:32) (cid:168) (cid:184) Length(cid:32) 157.942 (cid:169) 54.02 (cid:185) Click to View Mathcad Document Mathcad ® Enabled Content Copyright © 2012 Knovel Geometry and Breaking Forces of the Catenary (SI Units) Problem: To find the geometry and breaking forces of the catenary Created by Valery Ochkov Area 1: Disclaimer Area 2: User Notices Area 3: Method (cid:167) (cid:167)x(cid:16) x (cid:183) (cid:183) 0 The catenary function: y(cid:11)x(cid:15)(cid:3)x (cid:15)(cid:3)h(cid:15)(cid:3)a(cid:12)(cid:29)(cid:32) h(cid:14) a(cid:152)(cid:168)cosh(cid:168) (cid:184) (cid:16) 1(cid:184) 0 (cid:169) (cid:169) a (cid:185) (cid:185) h (cid:29)(cid:32) 15m 2 h (cid:29)(cid:32) 7m 1 L(cid:29)(cid:32) 30m Minimal catenary length l(cid:29)(cid:32) L2 (cid:14) (cid:11)h (cid:16) h (cid:12)2 (cid:32) 31.05m 1 2 Catenary length S > l S(cid:29)(cid:32) 39m Given Guess values x (cid:29)(cid:32) 12m h(cid:29)(cid:32) 1m 0 (cid:11) (cid:11) (cid:12) (cid:12) a(cid:29)(cid:32) 3m a(cid:29)(cid:32) root h (cid:16) y 0(cid:15)(cid:3)x (cid:15)(cid:3)h(cid:15)(cid:3)a (cid:15)(cid:3)a (cid:32) 12.89m 1 0 (cid:11) (cid:12) Fixing at the left end h = y 0(cid:15)(cid:3)x (cid:15)(cid:3)h(cid:15)(cid:3)a 1 0 (cid:11) (cid:12) Fixing on the right end h = y L(cid:15)(cid:3)x (cid:15)(cid:3)h(cid:15)(cid:3)a 2 0 L (cid:180) (cid:181) 2 Catenary length S = (cid:181) 1(cid:14) (cid:168)(cid:167)d y(cid:11)x(cid:15)(cid:3)x (cid:15)(cid:3)h(cid:15)(cid:3)a(cid:12)(cid:183)(cid:184) dx 0 (cid:181) (cid:169)dx (cid:185) (cid:182) 0 (cid:167)x (cid:183) 0 (cid:168) (cid:184) (cid:11) (cid:12) (cid:168) h (cid:184) (cid:29)(cid:32) Find x0(cid:15)(cid:3)h(cid:15)(cid:3)a x0(cid:32) 12.46m h(cid:32) 50.14mm (cid:168) (cid:184) (cid:169) a (cid:185) 15 x 0 10 5 h 0 5 10 15 20 25 30 kg lb Linear density of chain lpc(cid:29)(cid:32) 0.5 (cid:32) 0.336 m ft Area 5: Angles and forces calculation (cid:1)1(cid:32) (cid:16)50.445° <--Angles of inclination of the catenary at the it's ends--> (cid:1)2(cid:32) 63.316° Weight of the catenary G(cid:32) 19.5kgf F (cid:32) 9.568kgf F (cid:32) 13.568kgf 1 2 F (cid:32) 6.093kgf <--- Forces of tension on the catenary ends ---> F (cid:32) 6.093kgf x1 x2 F (cid:32) 7.377kgf F (cid:32) 12.123kgf y1 y2 Forces of breaking the chain Forces of breaking the catenary, kgf F 2 x 0 12 10 F 1 8 0 10 20 30 x, m