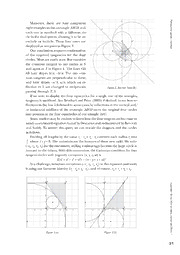
Pythagoras’ garden, revisited Frank R . Bernhart <farb45@gmail .com> H . Lee Price <tanutuva@rochester .rr .com> Mack and Czernezkyj (2010) have given an interesting account of primi- tive Pythagorean triples (PPTs) from a geometrical perspective. We wish here to enlarge on the role of the equicircles (incircle and three excircles), and show there is yet another family tree in Pythagoras’ garden. Where they begin with four equicircles, we begin with four tangent circles, attached to the corners of a rectangle based on the right triangle. Reflecting these circles in a certain line results in a congruent tangent cluster, having the same six points of tangency, orthogonal to the first four, and ultimately revealed as (jostled) equicircles! We then develop three celebrated families of triples by elementary means, and tinker with the sequencing rules until the classic Pythagorean family tree magically appears. Using a favourite set of four parameters to identify and tag triples, we find more circle secrets. A second and totally new family tree (in- vented by Price) is here debuted. We find it equally interesting and valuable, but so far lacking an adequate geometric interpretation. Getting started We begin with a few notational differences. Where the previous paper has a sequence A u (a, b, c) with a < b we use a matrix-like no- s tr a tation [a b c] using spaces rather than lia n commas. This is a triple of positive integers Se n io describing legs (a, b) and hypotenuse (c) r M of a right triangle ∆ABC. Moreover, a, c are ath e odd, b is even, and the greatest common m a divisor of the sides is one. Thus where they tics J o have (20, 21, 29), we have [21 20 29]. We u r n a state without proof that every right trian- l v o gle with rational sides is similar to one and l. 2 6 only one PPT. Figure 1 no . 1 29 e ric The example in Figure 1 is the venerable [3 4 5] triangle for definiteness, P dt & and we have established a coordinate system with C as origin, and rays CB, CA r a as positive x-axis and positive y-axis. Our figure shows three circles of radii h n er [1, 2, 3] centred on C, B, A and a fourth circle centred on D with radius 6, B where ADBC makes a rectangle. These are four mutually tangent circles. Generalisation is quite easy. Just put a = r + r , b = r + r , c = r + r (1.1) 1 2 1 3 1 3 The radii are positive integers because of the triangle inequality, and since a, c are odd and b is even (solve for the r to see this). Define r = r + r + r so 1 4 1 2 3 that (1.1) is equivalent to a = r – r , b = r – r , c = r – r (1.2) 4 3 4 2 4 1 Mutual tangency of four circles as in Figure 1 is now almost immediate. It is simply a matter of applying the six equations (1.1), (1.2) to the six line seg- ments determined by A, B, C, D. The Pythagorean identity a2 + b2 = c2 becomes r (r + r + r ) = r ⋅ r or even 1 1 2 3 2 3 more simply r ⋅ r = r ⋅ r . Two more easily verified forms of this fecund iden- 1 4 2 3 tity are (the first goes back to Dickson (1894); see Gerstein (2005) for history and applications): 2r 2 = (r – r )(r – r ), (a + b – c)2 = 2(c – a)(c – b) (1.3) 1 3 1 3 2 We add as a useful and easily proved fact, that in the sequence r , r , r , r 1 2 3 4 the values alternate odd/even or even/odd. Also r is smallest and r is largest. 1 4 What does this have to do with the equicircles of Mack and Czernezkyj? Everything. We reconsider Figure 1. These six points of tangency support a second set of four tangent circles, a general fact which Coxeter (1989) as- cribes to a schoolteacher named Beecroft. Though easily proved, we can take a nice shortcut because of the right triangle and get even more. The descending 45° line l in Figure 1 contains the diagonals of three suc- cessive squares (sides AL, LC, MB), and so must pass through four tangency points (a harmonic set). It happens that the other two points of tangency S, T define a segment for which l is the perpendicular bisector! This is an exercise in elementary analytic geometry. Here are some hints to make the work less tedious. The line equations are x + y = r for l and 1 x y + =1 a b for the hypotenuse line AB. The coordinates of S, T are easily found as weighted averages (or use simi- 1 o. lar triangles). This is because T divides AB in the ratio r : r , and S divides CD n 6 3 2 2 in the negative ratio(–r ) : r . ol. 1 4 rnal v S =r4C−r1D=−ar1, −br1, T =[r3B+r2A]=arr3, br2 u Jo c  c c  c  c c  s c mati The slope of ST computes to +1, and the midpoint lies on x + y = r . e 1 ath We now may conclude that reflection in l exchanges S with T and fixes M r the other four tangency points. The four circles, on reflection, give a congru- o ni e ent set of four circles, in fact the Beecroft dual configuration. Combining the S n a eight circles makes a beautiful diagram that we call the “Beecroft butterfly” ali r st (Figure 2). u A 30 P Moreover, there are four congruent yth a g right triangles in the rectangle ABCD, and o r a each one is matched with a different cir- s’ g a cle in the dual system, showing it to be an rd e n excircle or incircle. These four cases are , r e v displayed as two pairs in Figure 3. isite d Our conclusion requires confirmation of the required tangencies for the dual circles. Most are easily seen. But consider the common tangent to two circles at S and again at T in Figure 1. The lines CD, AB have slopes b/a, –b/a. The two com- mon tangents are perpendicular to these, and have slopes –a/b, a/b, which on re- flection in l are changed to reciprocals, Figure 2. Beecroft ‘butterfly’. passing through T, S. If we were to display the four equicircles for a single one of the triangles, tangency is sacrificed. See Bernhart and Price (2005) if desired, to see how re- flections in the line l followed in some cases by reflections in the vertical and/ or horizontal midlines of the rectangle ABCD move the original four circles into position as the four equicircles of our triangle ABC. Some readers may be curious to know how the four tangent circles come to satisfy a celebrated equation found by Descartes and rediscovered by Beecroft and Soddy. To answer this query we can rescale the diagram and the circles as follows. Dividing all lengths by the value r ⋅ r = r ⋅ r converts each radius r into 1 4 2 3 i 1 where i + j = 5. The curvatures are the inverses of these new radii. We write r j (–r , r , r , r ) for the curvatures, adding a minus sign because the large circle is 1 2 3 4 concave to the others. With this convention, the Cartesian condition for four tangent circles with (signed) curvatures (x, y, z, w) is 2(x2 + y2 + z2 + w2) = (x + y + z + w)2 As a challenge, substitute curvatures (–r , r , r , r ) in this equation and verify 1 2 3 4 it using our favourite identity (r ⋅ r = r ⋅ r ), and of course, r = r + r + r . 1 4 2 3 4 1 2 3 A u s tr a lia n S e n io r M a th e m a tic s J o u r n a l v o l. 2 6 n Figure 3 (a) Figure 3 (b) o . 1 31 e ric So the same four circles, moved around, can be a set of tangent circles, a P dt & second system of tangent circles (Figure 2), or the set of equicircles for ∆ABC. r a In a similar application, we can show that the Hero(n) formula for the area h n er G of the triangle becomes G2 = r ⋅ r ⋅ r ⋅ r or G = r ⋅ r = r ⋅ r . This is because B 1 2 3 4 1 4 2 3 the semiperimeter s and the other Heron factors are s = r , s – c = r , s – b = r , 4 1 2 s – a = r , which are but simple deductions from equations (1.1), (1.2). 3 Three families of Pythagorean triples Mack and Czernezkyj carry out a geometric construction of the Pythagorean Tree using each excircle. In three cases they have another PPT, and the sides (a', b', c') of the new triple are simple linear combinations of the sides (a, b, c) of the old. We will now sketch a way to do this, starting with simple questions. In our notation a, c are odd and b is even, and triple [3 4 5] consists of con- secutive integers. No other PPT has consecutive integers, but: F1. What about b + 1 = c ? F2. What about a + 2 = c ? F3. What about a = b + 1 or a + 1 = b ? Suppose that c – b = 1. Then a2 = c2 – b2 = (c + b)(c – b) = c + b. We find b, c by splitting the square of any odd number into “almost equal halves”. Thus a = 9 has square 81 = 40 + 41, and we have produced triple [9 40 41] which satisfies F1. Similarly suppose that c – a = 2. Accepting that consecutive odd numbers like a, c add to a multiple of four (easy number theory) we get b2 = c2 – a2 = (c + a)(c – a) = 2(c + a) is divisible by eight, implying that even leg b is divisible by four. We claim that if x is the integer between a, c then x =(1b)2. So take 1 2 any multiple of four, such as b = 12. The square of b = 6 lies between integers 2 a, c so we have produced triple [35 12 37] that satisfies F2. The two infinite families just described are ascribed to Pythagoras and Plato, respectively. The family which answers to F3 grows more rapidly, and requires some skill to ‘bag’. It was first securely bagged by Fermat, so we call it the Fermat family. Our approach came to us in connection with some facts concerning simple continued fractions and Pell equations, but we will take a less arduous path. Suppose that b – a = 1 or a – b = 1. Write {a, b} = {x, x + 1} to cover both cases. 1 o. A bit of algebra and the Pythagorean identity shows that (a + b)2 and 2c2 differ n 6 2 by one, i.e., (a + b)2 = (2x + 1)2 = A2 and B2 = c2 lead to (#1) A2 – 2B2 = –1. Trial ol. al v and error with small numbers finds a few solutions to (#1), and also solutions n ur to (#2) A2 – 2B2 = +1 form a series of “fractions” A/B. o cs J 1, 3, 7, 17, 41,  mati 1 2 5 12 29 e ath We will conveniently ignore the fact that these fractions have something to M r do with the square root of two, because that might be a public school bonus o ni e topic. Instead, we just scrutinise the numbers, until we serendipitously notice S n a that the sum (A + B) of a numerator and denominator equals the next de- ali r st nominator, and that each numerator A is the sum of its denominator B and u A 32 P the previous denominator, say B'. Differently put, we have stitched together yth a g short Fibonacci-style sequences. o r a 1, 1, 2, 3; 3, 2, 5, 7; 7, 5, 12, 17; 17, 12, 29, 41; … s’ g a In each ‘quartet’, the last two numbers are exchanged to begin the next rd e n quartet, and all quartets have the Fibonacci form (a, b, a + b, a + 2b) or equiv- , r e v alently (b – a, a, b, a + b). Query/challenge: do two adjacent values in the isite d quartets ever have a common factor >1? Our first concern is whether this ‘rule’ is just an accident, or a persistent x pattern. Given any fraction , we can use the alleged rule to go forward to y x+2y −x+2y , and, if x < 2y, we can go backward to . Now use elementary algebra x+y x−y x to show that if is a solution of (#1) (or of (#2)), then both the left hand and y −x+2y x+2y right hand fractions and are solutions of (#2) (or of (#1)). That is, x−y x+y solutions of the two cases alternate. Naturally, this is why we kept the two cases in tandem. But we knew the answer before opening the envelope to read the question. Given any solution to either case, we can back up with the rule until arriv- x ing at a fraction which fails the condition x < 2y. But then it is not hard to y argue that y is small enough that we must have one of the ad hoc small solu- tions already compiled by trial and error. This concludes the argument that our sequence, extended by the rule, necessarily finds all the answers to both cases (#1), (#2). Formula, formula For those who crave formulas, we can supply [(2n + 1) 2n(n + 1) (2n(n + 1)+1)] for the Pythagoras family, and [4n (4n2 – 1) (4n2 + 1)] for the Plato family. Both are easily found to square with our descriptions. We can also define two sequences (P) and (Q) having a generating pattern displayed as follows: (…, i i x, y, x + 2y, …). For the former we begin with (0, 1, …) and for the latter we begin with (1, 1, …). There exist exact formulas for both, too involved to pre- sent here. 1 1 Where P is odd, split Q into “halves” [ Q ], and [ Q + 1]. Here [.] is n n 2 n 2 n greatest integer function (or round down). Thus 41 gives 41 = 20 + 21, yield- 29 ing the Fermat family member[21 20 29]. Likewise, 239 gives 239 = 119 + 120 169 and thus another member, [119 120 169]. Since there are exact functions of A u n for P and Q , the same could be said of Fermat family triples. s n n tra lia n S e n Recursion is boss ior M a th e What we intend to do is play a bit with recursive patterns until something as- m a tounding happens. tics J o A simple geometric diagram (Figure 4) convinces us that the step from 52 u r n a to 72 is just 5 + 5 + 7 + 7. l v o l. 2 6 n o . 1 33 e c ri P & dt r a h n r e B Figure 4 More generally, we advance from [a b c] in the Pythagoras family to the next member [a' b' c'] as follows: (Pythagorus) a → a' = a + 2, b → b' = b + (a + a') = b + 2a + 2, c → c' = c + (a + a') = c + 2a + 2 Note that increase 2(a + a') is divided between b and c. Anyone quite satisfied with a formula may look at this askance. We claim that this supports a simple algorithm for converting one family member to the next. This is a recursive emphasis that will pay enormous dividends, given a further tweak. A geometric diagram similar to the last evaluates the step from 82 to 122. It gives the difference as (8 + 8 + 8 + 8) + (12 + 12 + 12 + 12) = 4(8 + 12). Thus recursively, when a, c each increase by b + b', 2(c + a) then increases by 4(b + b') as with b = 8 and b' = 12. (Plato) b → b' = b + 4, a → a' = a + (b + b') = a + 2b + 4, c → c' = c + (b + b') = c + 2b + 4 Finally, a Fermat member [a b c] is represented in the fraction sequence as a+b, or since we have assumed that a + b = 2x + 1, this fraction equals 2x+1. c c Generating two further steps by our simple rule produces a+b a+b+2c 3a+3b+4c 6x+3+4c → → = . c a+b+c 2a+2b+3c 2a+2b+33c We want to see this last fraction as a′+b′, where [a' b' c'] is the very next Fer- c′ mat triple. The almost equal halves of the numerator are 3x + 1 + 2c and 3x + 2 + 2c. Certainly one of these is the same as a + 2b + 2c and the other is 2a + b + 2c and since a, a' are odd and b, b' are even, the former must be a' and the latter must be b'. Thus 1 o. (Fermat) n 6 2 a → a' = a + 2b + 2c, b → b' = 2a + b + 2c, c → c' = 2a + 2b + 3c ol. v al n ur Checking the difference of the legs a', b' we find (a' – b') = (b – a). In other o J s words, the difference between the legs merely changes sign. c mati We have a nice little linear transformation/substitution with the following e ath pattern of coefficients, M r Fermat a b c o eni a′= 1 2 2 S an b′= 2 1 2 ali str c′= 2 2 3 u A 34 P put for convenience in a matrix-like table. yth a g There are coefficients but no constants, unlike what we obtained for o r a the Pythagoras and Fermat families. Therefore something wonderful hap- s’ g a pens. Let [a b c] be any PPT, not necessarily one of the Fermat family. We rd e n test [a' b' c'] by putting the above expressions into the Pythagorean equation: , r e v (a + 2b + 2c)2 + (2a + b + 2c)2 = (2a + 2b + 3c)2. This can be simplified, and isite d behold: it turns into the given equation a2 + b2 = c2. So applying this transfor- mation to an arbitrary PPT obtains another (that the triple is primitive is a small lemma). Moreover, the difference between the legs changes sign only. No special favours for Fermat Why can we not get the same generality for the other recursions? Only the constants are stopping us, so we get rid of them! In [Pythagoras] above, the constant 2 appears. But we know that c – b = 1 and thus 2(c – b) = 2. Replace each constant two by 2(c – b), then proceed as before. In [Plato] above, the constant 4 appears. Since we have c – a = 2, replace each four with 2(c – a), and proceed. When all the shouting is over, each of those linear transformations is ho- mogeneous (constant-free). Namely, just a linear combination of a, b, c. Again the coefficients can be put in a table. For the Pythagoras and Plato families we have Plato a b c Pythagoras a b c a′= −1 2 2 a′= 1 −22 2 b′= −2 1 2 b′= 2 −1 2 c′= −2 2 3 c′= 2 −2 3 Surprise: this is just the previous table, except that the first column (the second column) has changed sign. The three similar transformations apply to any primitive triple [a b c] to create three immediate successors, or ‘children’. This generates an infinite ternary tree. The three children can be arranged in several orders, but we prefer to put the Pythagoras-like child on the right c' – b' = c – b, the Plato-like child on the left c' – a' = c – a, and the Fermat-like child squarely in the middle b' – a' = a – b. The classic tree (Figure 5) is here presented like a family tree, growing down- A u ward, with triple [3 4 5] at the top, and the three families are infinite paths on s tr a the left edge (Plato), the right edge (Pythagoras) and straight down (Fermat). lia n S e n [3 4 5] ior M (cid:31) ↓ (cid:30) a th Plato Fermat Pythagoras em [15 8 17] [21 220 29] [5 12 13] atic s (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) J o u [35 12 37] [65 72 97] [33 56 65] [77 36 85] [119 120 169] [39 80 89] [45 28 53] [55 48 73] [7 24 25] rn a (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30)(cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) l v o l. 2 6 Figure 5. Classic tree. n o . 1 35 e ric For space reasons we will skip the lemma that every PPT different than P dt & [3 4 5] has a unique ‘parent’ with a smaller hypotenuse for which it is one of r a the three children. Given that, each PPT occurs once and once only on the h n er infinite family tree. B Our next job is to exhibit a four-parameter system that may be used to con- struct the usual tree, or, can be used to define an entirely new tree. Four very special parameters In the right triangle ABC with opposing sides a, b, c there are two acute angles at A, B. Now a simple geometric diagram can be used to compute the tangents of the half angles a, b. These are found to be b c −a a c −b = and = a+c b b+c a The four parameters we need are found by reducing the half-angle tangents to simplest fractions, to obtain a pair of numerators and denominators. Figure 6 For example, from [21 20 29] we have 29−21 2 = 20 5 29−20 3 and = 21 7 These four numbers happen to form a short Fibonacci sequence (3, 2, 5, 7) like the quartets we had in a previous section. We now put this aside, and develop our parameters carefully from the circle radii. 1 o. Equation r (r + r + r ) = r ⋅ r is the gift that keeps on giving. We divide by n 6 1 1 2 3 2 3 2 r ⋅ r and get ol. 2 3 rnal v r1r1+r1+r1=1 Jou r2r3 r2 r3 s c mati which has form xy + x + y = 1 for rational numbers x, y. Let the fractions after e Math reduction to lowest terms be x = qp andy = qp'' noting (since r1 ⋅ r4 = r2 ⋅ r3) that or x = q = r1 = r3 ni e p r r an S 2 4 ali r st u A 36 q' r r and that y = = 1 = 2 P p' r3 r4 ytha g o r a Thus, since the radii alternate in parity, qp'' has both parts odd, whereas x = qp s’ ga has one part even. But xy + x + y = 1 produces both rd e n p−q q' p' −q' 2q q , r = and = = ev p+q p' p' +q' 2p p isite d Equating numerators and denominators we have a sequence of four curious parameters: (q', q, p, p') = (p – q, q, p, p + q) This four-term sequence obeys the Fibonacci rule: q' + q = p, q + p = p'. We omit the easy verification that all four are relatively prime in pairs, and also that any two determine all four. Moreover, since reduced q r r x = = 1 = 3 p r r 2 4 one must have positive integers k, m such that r = kq, r = kp, r = mq, r = mp. 1 2 3 4 Any common factor of k, m must divide all r and thus a, b, c as well. We con- i clude that k, m are relatively prime. But then r k q' 1 = = r m p' 3 forces k = q', m = p'. In sum: r = qq', r = pq', r = qp', r = pp' (1.4) 1 2 3 4 In fact, one can choose any positive whole numbers q', q such that q' is odd and they have no common factors. The radii follow by (1.4) and the triple by (1.1). For example: (q', q) = (3, 4) → (p, p') = (7, 11) → (r , r , r , r ) = (12, 21, 44, 77) 1 2 3 4 → [a b c] = [33 56 65] Put G(x, y) = [(x2 – y2), 2xy, (x2 + y2)]. Then the PPT is equally G(p, q) or 1 G(p', q'). These are just the two standard parametric solutions for obtaining 2 x = q q' triples. We can say yet more about the fractions and . Figure 5 shows the p p' right triangle with two acute angles 2a and 2b. The half-angle tangent were found to be b (c −a) a (c −b) tanβ= = and tanα= = . (c+a) b (c+b) a A u Recall that a = r + r , b = r + r , c = r + r . The half-angle tangents are then s 1 2 1 3 2 3 tra r3 −r1, r2 −r1 lian S r +r r +r e 3 1 2 1 n io r M x = q aWned oqm' .i t the verification via r1(r1 + r2 + r3) = r2 ⋅ r3 that once again, we have athem p p' a tic s r r J o That is, 1 , 1 . u r r r na 2 3 l v o Generation of the three children of a given triple in terms of the four new l. 2 6 parameters is singularly simple as we now show. no . 1 37 e c Family trees using parameters ri P & dt r a We state without proof the easy result that if triple [a b c] has associated with h n er it the parameters (q', q, p, p') the three direct descendants of this triple (us- B ing the linear transformations given above) have parameter sequences of the form (q', p, •, •) (p', q, •, •) (p', p, •, •) In other words, q is changed to p, or q' is changed to p', or both. The last two elements in the sequence (•) have to be recomputed by the Fibonacci rule. A mnemonic for this is “flip one or both of the fractions q/p, q'/p', and save only the numerators”. This is clearer with an example. Parameter sequence (3, 2, 5, 7) goes with triple [21 20 20]. We change 3 to 7 or 2 to 5 or both at once. This gives (7, 2, …), (3, 5, …) (7, 5, …) which are completed by Fibonacci addition to (7, 2, 9, 11) (3, 5, 8, 13) (7, 5, 12, 17) [77 36 85] [39 80 89] [119 120 169] These three triples obtained from the parameters are the three children of [21 20 29]. One may check the unchanged differences: 21 – 20 = 120 – 119, 29 – 20 = 89 – 80, 29 – 21 = 85 – 77. Recall that r = qq' is the inradius. In the three children this has changed 1 to pq', qp', pp'. So each exradius r , r , r is ‘promoted’ in turn to be the new 2 3 4 inradius. This implies that no matter how we pick a path down the tree, we are always increasing the inradius. It is a bit uncertain who first realized that PPTs had a beautiful family tree, but a 1934 paper in Swedish could be the earliest (Berggren, 1934). One of us (Price, 2008) played with the sequence and found a totally new tree. Start by dropping parameters q, p. We are left with (q', •, •, p'). Move the last parameter p' left in the sequence in three ways: (q', •, p', •), (p', q', •, •), (q', p', •, •). Re-compute the missing two parameters. It turns out that this is a valid and different way to produce three direct descendants! To explain the following diagram, we need to say that the small box (we call it a Fibonacci Box) displays the generating parameters (half-angle tangents) in the left and right columns. The parameter sequence is coiled: start in the upper right corner and read counterclockwise. One may notice that for the  1 1  1   o.  2 3  n 6 [3 4 5] 2 ol. (cid:31) ↓ (cid:30) v nal  2 1   1 3   3 1  r u       Jo  3 5   4 5   4 7  s c [5 12 13] [15 8 17]] [7 24 25] ati m (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) (cid:31) ↓ (cid:30) e h Mat  4 1   1 5   5 1   2 3   3 5   5 33   6 1   1 7   7 1                    or  5 9   6 7   6 11   5 7   8 11   8 13   7 13   88 9   8 15  ni e [9 40 41] [35 112 37] [11 60 61] [21 20 299] [55 48 73] [39 80 89] [13 84 85] [63 16 65] [15 112 113] S n a (cid:31)↓(cid:30) (cid:31)(cid:31)↓(cid:30) (cid:31)↓(cid:30) (cid:31)↓(cid:30) (cid:31)↓(cid:30) (cid:31)↓(cid:30) (cid:31)↓(cid:30) (cid:31)↓(cid:30) (cid:31)↓↓(cid:30) ali r st Figure 7. The new tree (three generations). u A 38