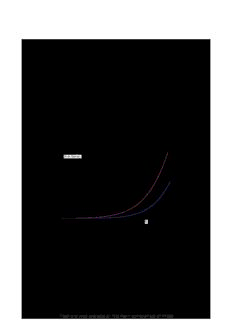
Mathematical Definition, Mapping, and Detection of (Anti)Fragility Nassim Nicholas Taleb and Raphael Douady † ⇤ November 2013 Forthcoming,QuantitativeFinance Weprovideamathematicaldefinitionoffragilityandantifragilityasnegativeorpositivesensitivitytoasemi-measureof dispersionandvolatility(avariantofnegativeorpositive"vega")andexaminethelinktononlineareffects. Weintegrate modelerror(andbiases)intothefragileorantifragilecontext. Unlikerisk,whichislinkedtopsychologicalnotionssuch as subjective preferences (hence cannot apply to a coffee cup) we offer a measure that is universal and concerns any object that has a probability distribution (whether such distribution is known or, critically, unknown). We propose a detectionoffragility,robustness,andantifragilityusingasingle"fast-and-frugal",model-free,probabilityfreeheuristic thatalsopicksupexposuretomodelerror. Theheuristiclendsitselftoimmediateimplementation,anduncovershidden risksrelatedtocompanysize,forecastingproblems,andbanktailexposures(itexplainstheforecastingbiases). While simpletoimplement,itimprovesonstresstestingandbypassesthecommonflawsinValue-at-Risk. 1 Introduction Prob Density K Ξ K,s"#$s" % x"’ f x )x ! " # ! " Λ!s_#$s""! " "& K Ξ K,s" % x"’ f x )x ! " # ! " Λ!s_"! " "& K The notions of fragility and antifragility were introduced in Taleb (2012). In short, fragility is related to how a systemsuffersfromthevariabilityofitsenvironmentbeyondacertainpresetthreshold(whenthresholdisK,itiscalled K-fragility),whileantifragilityreferstowhenitbenefitsfromthisvariability—inasimilarwayto“vega”ofanoptionor anonlinearpayoff,thatis,itssensitivitytovolatilityorsomesimilarmeasureofscaleofadistribution. Simply,acoffeecuponatablesuffersmorefromlargedeviationsthanfromthecumulativeeffectofsomeshocks— conditional on being unbroken, it has to suffer more from “tail” events than regular ones around the center of the distribution,the“atthemoney”category. Thisisthecaseofelementsofnaturethathavesurvived: conditionalonbeing in existence, then the class of events around the mean should matter considerably less than tail events, particularly whentheprobabilitiesdeclinefasterthantheinverseoftheharm,whichisthecaseofallusedmonomodalprobability distributions. Further,whathasexposuretotaileventssuffersfromuncertainty;typically,whensystems–abuilding,a bridge,anuclearplant,anairplane,orabankbalancesheet–aremaderobusttoacertainlevelofvariabilityandstress FormerTrader,flaneur,andNYU-Poly ⇤ †Centred’ÉconomiedelaSorbonne 1 Electronic copy available at: http://ssrn.com/abstract=2124595 TALEBandDOUADY MathematicalMappingof(Anti)Fragility butmayfailorcollapseifthislevelisexceeded, thentheyareparticularlyfragiletouncertaintyaboutthedistribution ofthestressor,hencetomodelerror,asthisuncertaintyincreasestheprobabilityofdippingbelowtherobustnesslevel, bringing a higher probability of collapse. In the opposite case, the natural selection of an evolutionary process is particularlyantifragile,indeed,amorevolatileenvironmentincreasesthesurvivalrateofrobustspeciesandeliminates thosewhosesuperiorityoverotherspeciesishighlydependentonenvironmentalparameters. Figure 1 show the “tail vega” sensitivity of an object calculated discretely at two different lower absolute mean deviations. Weuseforthepurposeoffragilityandantifragility,inplaceofmeasuresinL2 suchasstandarddeviations, whichrestrictthechoiceofprobabilitydistributions,thebroadermeasureofabsolutedeviation,cutintotwoparts: lower anduppersemi-deviationabovethedistributioncenter⌦. Thisarticleaimsatprovidingapropermathematicaldefinitionoffragility,robustness,andantifragilityandexamining howtheseapplytodifferentcaseswherethisnotionisapplicable. Intrinsic and Inherited Fragility: Our definition of fragility is two-fold. First, of concern is the intrinsic fragility, theshapeoftheprobabilitydistributionofavariableanditssensitivitytos-,aparametercontrollingtheleftsideofits owndistribution. Butwedonotoftendirectlyobservethestatisticaldistributionofobjects,and,ifwedid,itwouldbe difficulttomeasuretheirtail-vegasensitivity. Nordoweneedtospecifysuchdistribution: wecangaugetheresponse ofagivenobjecttothevolatilityofanexternalstressorthataffectsit. Forinstance,anoptionisusuallyanalyzedwith respecttothescaleofthedistributionofthe“underlying”security,notitsown;thefragilityofacoffeecupisdetermined as a response to a given source of randomness or stress; that of a house with respect of, among other sources, the distribution of earthquakes. This fragility coming from the effect of the underlying is called inherited fragility. The transfer function, which we present next, allows us to assess the effect, increase or decrease in fragility, coming from changesintheunderlyingsourceofstress. Transfer Function: A nonlinear exposure to a certain source of randomness maps into tail-vega sensitivity (hence fragility). Weprovethat InheritedFragility Concavityinexposureontheleftsideofthedistribution andbuildH,atransferfunctiongivin,ganexactmappingoftailvegasensitivitytothesecondderivativeofafunction. Thetransferfunctionwillallowustoprobepartsofthedistributionandgenerateafragility-detectionheuristiccovering bothphysicalfragilityandmodelerror. 1.1 Fragility As Separate Risk From Psychological Preferences Avoidance of the Psychological: We start from the definition of fragility as tail vega sensitivity, and end up with nonlinearityasanecessaryattributeofthesourceofsuchfragilityintheinheritedcase—acauseofthediseaserather than the disease itself. However, there is a long literature by economists and decision scientists embedding risk into psychologicalpreferences—historically,riskhasbeendescribedasderivedfromriskaversionasaresultofthestructureof choicesunderuncertaintywithaconcavityofthemuddledconceptof“utility”ofpayoff,seePratt(1964),Arrow(1965), Rothchild and Stiglitz(1970,1971). But this “utility” business never led anywhere except the circularity, expressed by MachinaandRothschild(2008),“riskiswhatrisk-avertershate.” Indeedlimitingrisktoaversiontoconcavityofchoices isaquiteunhappyresult—theutilitycurvecannotbepossiblymonotoneconcave,butrather,likeeverythinginnature necessarilyboundedonbothsides,theleftandtheright,convex-concaveand,asKahnemanandTversky(1979)have debunked,bothpathdependentandmixedinitsnonlinearity. Beyond Jensen’s Inequality: Furthermore, the economics and decision-theory literature reposes on the effect of Jensen’s inequality, an analysis which requires monotone convex or concave transformations —in fact limited to the expectationoperator. Theworldisunfortunatelymorecomplicatedinitsnonlinearities. Thankstothetransferfunction, whichfocusesonthetails,wecanaccommodatesituationswherethesourceisnotmerelyconvex,butconvex-concave and any other form of mixed nonlinearities common in exposures, which includes nonlinear dose-response in biology. For instance, the application of the transfer function to the Kahneman-Tversky value function, convex in the negative domain and concave in the positive one, shows that its decreases fragility in the left tail (hence more robustness) and reduces the effect of the right tail as well (also more robustness), which allows to assert that we are psychologically “morerobust”tochangesinwealththanimpliedfromthedistributionofsuchwealth, whichhappenstobeextremely fat-tailed. c 2013N.N.TalebandR.Douady 2 November2013 � Electronic copy available at: http://ssrn.com/abstract=2124595 TALEBandDOUADY MathematicalMappingof(Anti)Fragility Accordingly,ourapproachreliesonnonlinearityofexposureasdetectionofthevega-sensitivity,notasadefinition of fragility. And nonlinearity in a source of stress is necessarily associated with fragility. Clearly, a coffee cup, a house orabridgedon’thavepsychologicalpreferences, subjectiveutility, etc. Yettheyareconcaveintheirreactiontoharm: simply,takingzasastressleveland⇧(z)theharmfunction,itsufficestoseethat,withn>1, ⇧(nz)<n⇧(z)forall0<nz<Z⇤ where Z isthelevel(notnecessarilyspecified)atwhichtheitemisbroken. Suchinequalityleadsto⇧(z)havinga ⇤ negativesecondderivativeattheinitialvaluez. So if a coffee cup is less harmed by n times a stressor of intensity Z than once a stressor of nZ, then harm (as a negativefunction)needstobeconcavetostressorsuptothepointofbreaking;suchstrictureisimposedbythestructure ofsurvivalprobabilitiesandthedistributionofharmfulevents,andhasnothingtodowithsubjectiveutilityorsomeother figments. Justaswithalargestonehurtingmorethantheequivalentweightinpebbles, if, forahuman, jumpingone millimetercausedanexactlinearfractionofthedamageof,say,jumpingtothegroundfromthirtyfeet,thentheperson wouldbealreadydeadfromcumulativeharm. Actuallyasimplecomputationshowsthathewouldhaveexpiredwithin hoursfromtouchingobjectsorpacinginhislivingroom,giventhemultitudeofsuchstressorsandtheirtotaleffect. The fragilitythatcomesfromlinearityisimmediatelyvisible,soweruleitoutbecausetheobjectwouldbealreadybroken andthepersonalreadydead. Therelativefrequencyofordinaryeventscomparedtoextremeeventsisthedeterminant. Inthefinancialmarkets,thereareatleasttenthousandtimesmoreeventsof0.1%deviationsthaneventsof10%. There arecloseto8,000micro-earthquakesdailyonplanetearth,thatis,thosebelow2ontheRichterscale—about3million ayear. Thesearetotallyharmless,and,with3millionperyear,youwouldneedthemtobeso. Butshocksofintensity 6 and higher on the scale make the newspapers. Accordingly, we are necessarily immune to the cumulative effect of small deviations, or shocks of very small magnitude, which implies that these affect us disproportionally less (that is, nonlinearlyless)thanlargerones. Modelerrorisnotnecessarilymeanpreserving. s-,thelowerabsolutesemi-deviationdoesnotjustexpresschanges inoveralldispersioninthedistribution,suchasforinstancethe“scaling”case,butalsochangesinthemean,i.e. when theuppersemi-deviationfrom⌦toinfinityisinvariant,orevendeclineinacompensatorymannertomaketheoverall meanabsolutedeviationunchanged. Thiswouldbethecasewhenweshiftthedistributioninsteadofrescalingit. Thus thesamevega-sensitivitycanalsoexpresssensitivitytoastressor(doseincrease)inmedicineorotherfieldsinitseffect oneithertail. Thuss (l)willallowustoexpressthesensitivitytothe“disordercluster”(Taleb,2012): i)uncertainty,ii) � variability,iii)imperfect,incompleteknowledge,iv)chance,v)chaos,vi)volatility,vii)disorder,viii)entropy,ix)time, x)theunknown,xi)randomness,xii)turmoil,xiii)stressor,xiv)error,xv)dispersionofoutcomes. DETECTION HEURISTIC Finally,thankstothetransferfunction,thispaperproposesariskheuristicthat"works"indetectingfragilityevenif weusethewrongmodel/pricingmethod/probabilitydistribution. Themainideaisthatawrongrulerwillnotmeasure theheightof achild;butitcancertainlytellusif heisgrowing. Sincerisksinthetailsmaptononlinearities(concavity of exposure), second order effects reveal fragility, particularly in the tails where they map to large tail exposures, as revealedthroughperturbationanalysis. Moregenerallyeverynonlinearfunctionwillproducesomekindofpositiveor negativeexposurestovolatilityforsomepartsofthedistribution. 1.2 Fragility and Model Error Aswesawthisdefinitionoffragilityextendstomodelerror,assomemodelsproducenegativesensitivitytouncertainty, in addition to effects and biases under variability. So, beyond physical fragility, the same approach measures model fragility, based on the difference between a point estimate and stochastic value (i.e., full distribution). Increasing the variability(say,variance)oftheestimatedvalue(butnotthemean),mayleadtoone-sidedeffectonthemodel—justas anincreaseofvolatilitycausesporcelaincupstobreak. Hencesensitivitytothevolatilityofsuchvalue,the“vega”ofthe modelwithrespecttosuchvalueisnodifferentfromthevegaofotherpayoffs. Forinstance, themisuseofthin-tailed distributions (say Gaussian) appears immediately through perturbation of the standard deviation, no longer used as pointestimate,butasadistributionwithitsownvariance. Forinstance,itcanbeshownhowfat-tailed(e.g. power-law tailed) probability distributions can be expressed by simple nested perturbation and mixing of Gaussian ones. Such a c 2013N.N.TalebandR.Douady 3 November2013 � Electronic copy available at: http://ssrn.com/abstract=2124595 TALEBandDOUADY MathematicalMappingof(Anti)Fragility Figure1: Disproportionateeffectoftaileventsonnonlinearexposures,illustratingthenecessarycharacterofthenonlinearityoftheharm functionandshowinghowwecanextrapolateoutsidethemodeltoprobeunseenfragility. representationpinpointsthefragilityofawrongprobabilitymodelanditsconsequencesintermsofunderestimationof risks,stresstestsandsimilarmatters. 1.3 Antifragility It is not quite the mirror image of fragility, as it implies positive vega above some threshold in the positive tail of the distributionandabsenceoffragilityinthelefttail,whichleadstoadistributionthatisskewedright. FragilityandTransferTheorems Table1introducestheExhaustiveTaxonomyofallPossiblePayoffsy=f(x) ThecentralTable,Table1introducestheexhaustivemapofpossibleoutcomes,with4mutuallyexclusivecategories of payoffs. Our steps in the rest of the paper are as follows: a. We provide a mathematical definition of fragility, robustnessandantifragility. b. Wepresenttheproblemofmeasuringtailrisksandshowthepresenceofseverebiases attending the estimation of small probability and its nonlinearity (convexity) to parametric (and other) perturbations. c. Weexpresstheconceptofmodelfragilityintermsoflefttailexposure,andshowcorrespondencetotheconcavityof thepayofffromarandomvariable. d. Finally,wepresentoursimpleheuristictodetectthepossibilityofbothfragility andmodelerroracrossabroadrangeofprobabilisticestimations. Conceptually,fragilityresidesinthefactthatasmall–oratleastreasonable–uncertaintyonthemacro-parameter ofadistributionmayhavedramaticconsequencesontheresultofagivenstresstest,oronsomemeasurethatdepends onthelefttailofthedistribution, suchasanout-of-the-moneyoption. Thishypersensitivityofwhatweliketocallan “outofthemoneyputprice”tothemacro-parameter, whichissomemeasureofthevolatilityofthedistributionofthe underlyingsourceofrandomness. Formally,fragilityisdefinedasthesensitivityoftheleft-tailshortfall(non-conditionedbyprobability)belowacertain thresholdKtotheoverallleftsemi-deviationofthedistribution. Examples i- Aporcelaincoffeecupsubjectedto randomdailystressorsfromuse. c 2013N.N.TalebandR.Douady 4 November2013 � TALEBandDOUADY MathematicalMappingof(Anti)Fragility Table1: PayoffsandMixedNonlinearities Type Condition Left Tail Right Tail Nonlinear Derivatives Effect of fa- (Loss (Gain Do- Payoff Func- Equivalent tailedness of Domain) main) tion y = f(x) (Taleb,1997) f(x) compared "derivative" toprimitivex. where x is a random vari- able Type Fragile Fat (reg- Fat Mixed concave Long up-vega, More fragility 1 (type1) ular or left,convexright shortdown-vega if absorbing absorbing (fence) barrier, neutral barrier) otherwise Type Fragile Thin Thin Concave Shortvega Morefragility 2 (type2) Type Robust Thin Thin Mixed convex Short up - vega, Noeffect 3 left, concave longdown-vega right (digital, sigmoid) Type Antifragile Thin Fat Convex Longvega More an- 4 (thicker tifragility thanleft) ii- Taildistributioninthefunctionofthearrivaltimeofanaircraft. iii- Hidden risks of famine to a population subjected to monoculture —or, more generally, fragilizing errors in the applicationofRicardo’scomparativeadvantagewithouttakingintoaccountsecondordereffects. iv- Hiddentailexposurestobudgetdeficits’nonlinearitiestounemployment. v- Hiddentailexposurefromdependenceonasourceofenergy,etc. (“squeezabilityargument”). 1.4 Tail Vega Sensitivity Weconstructameasureof“vega”inthetailsofthedistributionthatdependsonthevariationsof s,thesemi-deviation belowacertainlevelW,choseninthe L1norminordertoensureitsexistenceunder“fattailed”distributionswithfinite firstsemi-moment. InfactswouldexistasameasureeveninthecaseofinfinitemomentstotherightsideofW. LetX bearandomvariable,thedistributionofwhichisoneamongaone-parameterfamilyofpdf f�,� I R. We considerafixedreferencevalue⌦and,fromthisreference,theleft-semi-absolutedeviation: 2 ⇢ ⌦ s�(�)= (⌦ x)f�(x)dx � Z �1 Weassumethat� s–(�)iscontinuous,strictlyincreasingandspansthewholerangeR =[0, + ),sothatwemay + use the left-semi-a!bsolute deviation s– as a parameter by considering the inverse function �(s) :1R I, defined by + s�(�(s))=sfors R+. ! Thiscondition2isforinstancesatisfiedif,foranygivenx<⌦,theprobabilityisacontinuousandincreasingfunction of�. Indeed,denoting x F�(x)=Pf�(X <x)= f�(t)dt, Z �1 anintegrationbypartyields: ⌦ s�(�)= F�(x)dx Z �1 c 2013N.N.TalebandR.Douady 5 November2013 � TALEBandDOUADY MathematicalMappingof(Anti)Fragility Thisisthecasewhen�isascalingparameter,i.e.,X ⌦+ �(X1 ⌦)indeedonehasinthiscase ⇠ � x ⌦ F�(x)=F1 ⌦+ �� , Å ã @@F��(x)= ⌦��2x f�(x)ands�(�)=�s�(1). It is also the case when � is a shifting parameter, i.e. X X0 � , indeed, in this case F�(x) = F0(x +�) and @@s��(x)=F�(⌦). ⇠ � ForK <⌦ands R+,let: 2 K ⇠(K,s�)= (⌦ x)f�(s )(x)dx � � Z �1 Inparticular,⇠(⌦,s–)=s–. Weassume,inafirststep,thatthefunction⇠(K,s–)isdifferentiableon( ,⌦] R . + TheK-left-tail-vegasensitivityofX atstresslevelK <⌦anddeviationlevels�>0forthepdf f� is: �1 ⇥ V(X,f�,K,s�)= @@s⇠(K,s�)= ⌦ (⌦ x)@@f��)dx dds�� �1 (1) � ÇZ � åÅ ã �1 Astheinmanypracticalinstanceswherethresholdeffectsareinvolved,itmayoccurthat⇠doesnotdependsmoothly ons–. Wethereforealsodefineafinitedifferenceversionofthevega-sensitivityasfollows: 1 V(X,f�,K,s�)= 2�s ⇠(K,s�+�s) ⇠(K,s� �s) � � � � K = (⌦ x)f�(s�+�s)(x)� f�(s���s)(x)dx � 2�s Z �1 Henceomittingtheinput�simplicitlyassumesthat�s 0. Notethat⇠(K,s�)=�E(X|X <K)Pf�(X <K). Itcanbe!decomposedintotwoparts: ⇠ K,s�(�) =(⌦ K)F�(K)+P�(K) � � � K P�(K)= (K x)f�(x)dx � Z �1 Wherethefirstpart(⌦ K)F�(K)isproportionaltotheprobabilityofthevariablebeingbelowthestresslevelKandthe secondpartP�(K)isthe�expectationoftheamountbywhichX isbelowK(counting0whenitisnot). Makingaparallel withfinancialoptions,whiles–(�)isa“putat-the-money”,⇠(K,s–)isthesumofaputstruckatK andadigitalputalso struckatK withamount⌦–K;itcanequivalentlybeseenasaputstruckat⌦withadown-and-inEuropeanbarrierat K. Letting�=�(s–)andintegratingbypartyields K ⌦ ⇠ K,s�(�) =(⌦ K)F�(K)+ F�(x)dx = F�K(x)dx (2) � Z Z � � �1 �1 Where F�K(x)=F�(min(x,K))=min(F�(x),F�(K)),sothat @⇠ ⌦ @@F��K(x)dx V(X,f�,K,s�)= @s(K,s�)= R�⌦1 @@F��(x)dx (3) �1 Forfinitedifferences R 1 ⌦ V(X,f�,K,s�,�s)= 2�s �F�K,�s(x)dx Z �1 c 2013N.N.TalebandR.Douady 6 November2013 � TALEBandDOUADY MathematicalMappingof(Anti)Fragility Where�+ and� aresuchthats(�+)=s +�s,s(� )=s �sand�FK (x)=FK (x) FK (x). s �s s� � �s� �� �,�s �s+ � �s� 2 Mathematical Expression of Fragility In essence, fragility is the sensitivity of a given risk measure to an error in the estimation of the (possibly one-sided) deviationparameterofadistribution, especiallyduetothefactthattheriskmeasureinvolvespartsofthedistribution –tails–thatareawayfromtheportionusedforestimation. Theriskmeasurethenassumescertainextrapolationrules that have first order consequences. These consequences are even more amplified when the risk measure applies to a variablethatisderivedfromthatusedforestimation,whentherelationbetweenthetwovariablesisstronglynonlinear, asisoftenthecase. 2.1 Definition of Fragility: The Intrinsic Case Thelocalfragilityofarandomvariable X dependingonparameter�,atstresslevelKandsemi-deviationlevels–(�)with � pdf f� isitsK-left-tailedsemi-vegasensitivityV(X,f�,K,s�). The finite-difference fragility of X� at stress level K and semi-deviation level s�(�) �s with pdf f� is its K-left-tailed finite-differencesemi-vegasensitivityV(X,f�,K,s�,�s). ± Inthisdefinition,thefragilityreliesintheunsaidassumptionsmadewhenextrapolatingthedistributionofX from � areas used to estimate the semi-absolute deviation s–(�), around ⌦, to areas around K on which the risk measure ⇠ depends. 2.2 Definition of Fragility: The Inherited Case Next we consider the particular case where a random variable Y = '(X) depends on another source of risk X, itself subject to a parameter �. Let us keep the above notations for X, while we denote by g� the pdf of Y,⌦Y = '(⌦) and c 2013N.N.TalebandR.Douady 7 November2013 � TALEBandDOUADY MathematicalMappingof(Anti)Fragility u (�)theleft-semi-deviationofY.Givena“strike”level � L='(K),letusdefine,asinthecaseofX : K ⇣ L,u�(�) = (⌦Y y)g�(y)dy � Z The inherited fragility of Y with respect to X�at stress�level�L1= '(K) and left-semi-deviation level s–(�) of X is the partial derivative: @⇣ K @g ds 1 VX Y,g�,L,s�(�) = @s L,u�(�) = (⌦Y Y) @��(y)dy d�� � (4) ÇZ � åÅ ã � � � � �1 NotethatthestresslevelandthepdfaredefinedforthevariableY,buttheparameterwhichisusedfordifferentiation is the left-semi-absolute deviation of X, s–(�). Indeed, in this process, one first measures the distribution of X and its left-semi-absolutedeviation,thenthefunction' isapplied,usingsomemathematicalmodelofY withrespecttoX and theriskmeasure⇣isestimated. Ifanerrorismadewhenmeasurings–(�),itsimpactontheriskmeasureofYisamplified bytheratiogivenbythe“inheritedfragility”. Onceagain,onemayusefinitedifferencesanddefinethefinite-differenceinheritedfragilityofY withrespecttoX, byreplacing,intheaboveequation,differentiationbyfinitedifferencesbetweenvalues�+ and�–,wheres–(�+)=s–+ �sands–(�–)=s– –�s. 3 Effect of Nonlinearity on Intrinsic Fragility Let us study the case of a random variable Y = '(X); the pdf g� of which also depends on parameter �, related to a variable X by the nonlinear function '. We are now interested in comparing their intrinsic fragilities. We shall say, for instance, that Y is more fragile at the stress level L and left-semi-deviation level u (�) than the random variable � X, at stress level K and left-semi-deviation level s�(�) if the L-left-tailed semi-vega sensitivity of Y� is higher than the K-left-tailedsemi-vegasensitivityofX : � V(Y,g�,L,µ�)>V(X,f�,K,s�) Onemayusefinitedifferencestocomparethefragilityoftworandomvariables:V(Y,g�,L,�µ)>V(X,f�,K,�s). In thiscase,finitevariationsmustbecomparableinsize,namely�u/u– =�s/s–. Let us assume, to start, that ' is differentiable, strictly increasing and scaled so that ⌦Y = '(⌦) = ⌦. We also assumethat,foranygivenx<⌦, @@F��(x)>0. Inthiscase,asobservedabove,� s–(�)isalsoincreasing. LetusdenoteGy(y)=Pg�(Y < y).!Wehave: G�(�(x))=Pg�(Y <�(y))=Pf�(X <x)=F�(x). Hence,if⇣(L,u–)denotestheequivalentof⇠(K,s–)withvariable(Y,g�)insteadof(X,f�),wehave: ⌦ d� ⇣ L,u�(�) = F�K(x)dx(x)dx Z � � �1 Because' isincreasingandmin('(x),'(K))='(min(x,K)).Inparticular ⌦ d� µ�(�)=⇣ ⌦,µ�(�) = F�K(x)dx (x)dx Z � � �1 TheL-left-tail-vegasensitivityofY istherefore: ⌦ @@F��K(x)dd�x(x)dx V Y,g�,L,u�(�) = R�⌦1 @@F��(x)dd�x(x)dx � � �1 Forfinitevariations: R c 2013N.N.TalebandR.Douady 8 November2013 � TALEBandDOUADY MathematicalMappingof(Anti)Fragility 1 ⌦ d� V(Y,g�,L,u�(�),�u)= 2�u �F�K,�u(x)dx(x)dx Z �1 Where�+ and� aresuchthatu(�+ )=u +�u,u(�+ )=u �uand FK (x)=FK (x) FK (x). Next,Theu�orem1�up�roveshowaconcauv�etran�sformation'u�(x)of�a�randomvar�i,a�bulexpro�d+uuces�frag��uility. THEOREM 1(FRAGILITY TRANSFER THEOREM) Let, with the above notations, ' : R R be a twice differentiable function such that '(⌦) = ⌦ and for any x < ⌦, dd'x(x)>0. TherandomvariableY ='(!X)ismorefragileatlevelL='(K)andpdf glambda thanXatlevelKandpdf f�if,andonlyif,onehas: ⌦ d2' HK(x) (x)dx <0 � dx2 Z �1 Where @PK @PK @P @P HK(x)= � (x) � (⌦) �(x) �(⌦) � @� @� @� @� � � � andwhere x P�(x)= F�(t)dt Z �1 isthepriceofthe“putoption”onX�with“strike”xand x PK(x)= FK(t)dt � � Z �1 isthatofa“putoption”with“strike”xand“Europeandown-and-inbarrier”atK. H can be seen as a transfer function, expressed as the difference between two ratios. For a given level x of the random variable on the left hand side of ⌦, the second one is the ratio of the vega of a put struck at x normalized by thatofaput“atthemoney”(i.e. struckat⌦),whilethefirstoneisthesameratio,butwhereputsstruckatxand⌦are “Europeandown-and-inoptions”withtriggeringbarrieratthelevelK. Proof LetIX� = ⌦ @@F��(x)dx,IXK� = ⌦ @@F��K(x)dx,andIY� = ⌦ @@F��(x)dd'x(x)dx. OnehasOnehasV(X,f�,K,s�(�))= IXK� IX�andVR(Y�1,g�,L,u�(�))=IYL�RI�Y1�hence: R�1 ¿ ¿ IL IK IK IL I V(Y,g�,L,u�(�))�V(X,f�,K,s�(�))= IYY�� � IXX�� = IXY�� ÇIXYK�� � IXY��å (5) Therefore,becausethefourintegralsarepositive,Therefore,becausethefourintegralsarepositive, V(Y,g�,L,u�(�)) V(X,f�,K,s�(�)) � IL IK I I . Y� X�� Y� X� Ontheotherhand,wehave IX� = @@P��(⌦)IXK� = @@P��K(⌦)¿and � ⌦ @F d' @P d' ⌦ @P d2' I = �(x) (x)dx = �(⌦) (⌦) �(x) (x)dx (6) Y� @� dx @� dx � @� dx2 Z Z �1 �1 ⌦ @FK d' @PK d' ⌦ @PK d2' IL = � (x) (x)dx = � (⌦) (⌦) � (x) (x)dx (7) Y� @� dx @� dx � @� dx2 Z Z �1 �1 c 2013N.N.TalebandR.Douady 9 November2013 � TALEBandDOUADY MathematicalMappingof(Anti)Fragility Anelementarycalculationyields: IYL� IY� = @P�K(⌦) �1 ⌦ @P�K(x)d2'dx+ @P�(⌦) �1 ⌦ @P�(x)d2'dx = ⌦ HK(x)d2'dx. (8) IXK� � IX� �✓ @� ◆ Z @� dx2 ✓ @� ◆ Z @� dx2 �Z � dx2 �1 �1 �1 LetusnowexaminethepropertiesofthefunctionH�K(x). For x K,wehave @@P��K(x)= @@P��(x)>0(thepositivityis aconsequenceofthatof @@F��),thereforeH�K(x)hasthesamesignas @P @PK �(⌦) � (⌦). @� @� � Asthisisastrictinequality,itextendstoanintervalontherighthandsideofK,say(˘ ,K]withK <K <.Butonthe otherhand: 1 @P @PK ⌦ @F @F �(⌦) � (⌦)= �(x)dx (⌦ K) �(K) @� @� @� @� � ZK � � ForKnegativeenough, @@F��(K)issmallerthanitsaveragevalueovertheinterval[K,⌦],hence @P @PK �(⌦) � (⌦)>0. @� @� � Wehaveproventhefollowingtheorem. THEOREM 2(FRAGILITY EXACERBATION THEOREM) Withtheabovenotations,thereexistsathreshold⇥�<⌦suchthat,if K ⇥� then H�K(x)>0forx (– ,�]with K<lambda<⌦. Asaconsequence,ifthechangeofvariable'isconcave_on ( ,�]andlinearon2[�1,⌦],thenY ismorefragileatL='(K)thanXatK. �1 Onecanprovethat,foramonomodaldistribution,⇥�<�<⌦(seediscussionbelow),sowhateverthestresslevel K belowthethreshold⇥�,itsufficesthatthechangeofvariable' beconcaveontheinterval(– ,⇥�]andlinearon [⇥�,⌦]forY tobecomemorefragileatLthanX atK.Inpractice,aslongasthechangeofvaria1bleisconcavearound thestresslevelK andhaslimitedconvexity/concavityawayfromK,thefragilityofY isgreaterthanthatofX. Figure 3 shows the shape of HK(x) in the case of a Gaussian distribution where � is a simple scaling parameter � (� is the standard deviation �) and ⌦ = 0. We represented K = –2� while in this Gaussian case, ⇥� = –1.585�. DISCUSSION Monomodalcase Wesaythatthefamilyofdistributions(f�)isleft-monomodalifthereexistsK�<⌦suchthat @@f�� æ0on(– ,�]and @@f�� ∂0on[µ�,⌦]. Inthiscase @@P�� isaconvexfunctiononthelefthalf-line(– ,µ�],thenconcaveaftert1heinflexion pointµ�. ForK µ�,thefunction @@P��K coincideswith @@P�� on(– ,K],thenis1alinearextension,followingthetangent to the graph of @@P�� in K (see graph below). The value of @@P��K(⌦1) corresponds to the intersection point of this tangent @P withtheverticalaxis. ItincreaseswithK,from0whenK – toavalueabove @��(⌦)whenK =µ�. Thethreshold @PK ! 1@P @P @P ⇥�correspondstotheuniquevalueofK suchthat @��(⌦)= @��(⌦). WhenK <⇥�thenG�(x)= @��(x) @��(⌦)and G�K(x)= @@P��K(x) @@P��K(⌦) are functions such that G�(⌦)= G�K(⌦)=1 and which are proportional for x ¿K, the latter  . c 2013N.N.TalebandR.Douady 10 November2013 �